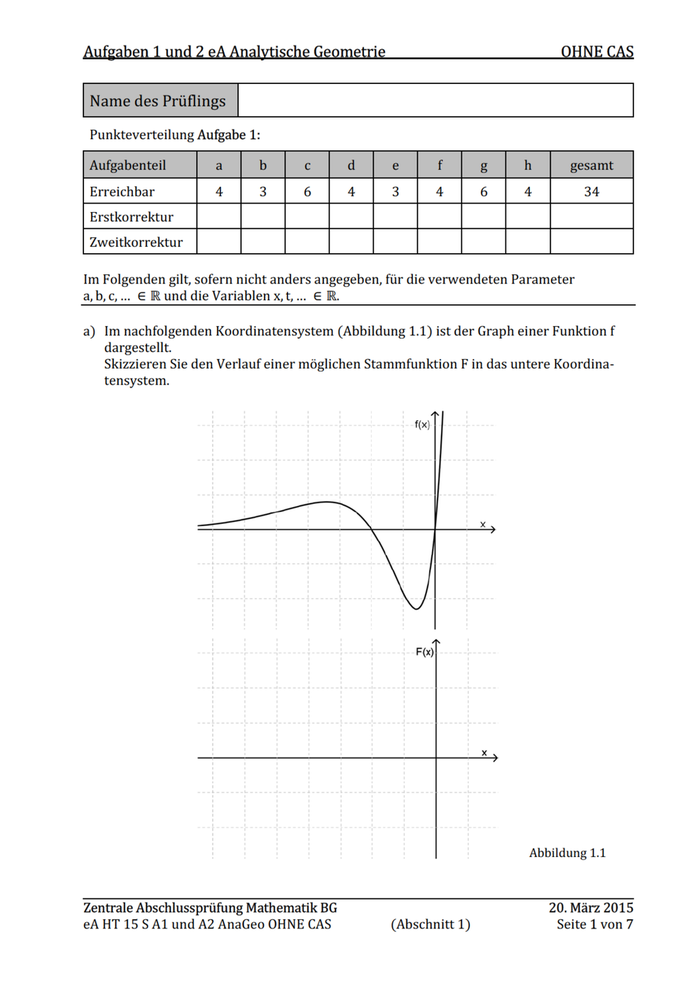
Auf nl und 2 eA Analytisch metri HNE

Punkteverteilung Aufgabe 1:

Aufgabenteil

Erreichbar
Erstkorrektur

Zweitkorrektur

 

Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter
a,b,c,... € Runddie Variablen x,t,... € R.

a) Im nachfolgenden Koordinatensystem (Abbildung 1.1) ist der Graph einer Funktion f
dargestellt.
Skizzieren Sie den Verlauf einer möglichen Stammfunktion F in das untere Koordina-

tensystem.
fix) |
Fix
x
Abbildung 1.1

Zentrale Abschlussprüfung Mathematik BG 20. März 2015
eAHT 15 S Al und A2 AnaGeo OHNE CAS (Abschnitt 1) Seite 1von 7

Auf nl und2eA Analvti metri HN

b) Bestimmen Sie den Parameter a für die Funktion fa mit der Funktionsgleichung

3

f,x)=a'x®-x mita>0

so, dass der Graph der Funktion fa mit der x-Achse im IV. Quadranten einen
Flächeninhalt von 0,25 Flächeneinheiten (FE) einschließt.

c) Der Graph einer ganzrationalen Funktion f mit der allgemeinen Funktionsgleichung
f(x) =a’x*+b-x®+c:'x?+d:x+ e verläuft achsensymmetrisch zur Ordinatenachse,
hat im Punkt A(2]5) ein lokales Maximum und an der Stellex = —1 die Steigung
m=-—6.

Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind und begründen Sie.

Der zugehörige Funktionsterm
kann nicht eindeutig bestimmt
werden, da die Anzahl der ge-
gebenen Bedingungen zu ge-
ring ist.

Aus den gegebenen Bedingun-
gen lässt sich unter anderem
folgende Gleichung aufstellen:
d=0.

 

Um die Koeffizienten der
Funktion f bestimmen zu
können, wird die zweite
Ableitungsfunktion benötigt.

d) Gegeben ist die Funktion f} mit der Funktionsgleichung
f{(x) = cos(2(x+1)) +t.

Geben Sie an, für welche Werte des Parameters t der Graph innerhalb einer Periode die
Abszissenachse zweimal oder gar nicht schneidet.

Ermitteln Sie für t= 1 die Koordinaten der Berührpunkte mit der Abszissenachse in-
nerhalb des Intervalls [0; 2].

Zentrale Abschlussprüfung Mathematik BG 20. März 2015
eAHT 15 SA1 und A2 AnaGeo OHNE CAS (Abschnitt 1) Seite 2 von 7

Auf nl und2eA Analvti metri HN

1 -5
e) Gegeben sind die Vektoren OA = (‘) und AB = (-25) sowie der Punkt

2 3
C(-2| - 2,5]1,5).

Bestimmen Sie die Koordinaten des Vektors BC.

fJ) Gegeben sind die zwei linear unabhängigen Vektoren ä und b.

Prüfen Sie, ob auch die Vektoren € = 2ä+bundd = -ä linear unabhängig sind.

5 a
g) Im R? ist die Geradenschar g.:X = () +r: ( 1 ) gegeben.
3 l+ta

Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind und begründen Sie Ihre
Entscheidung.

Entscheidung und Begründung

Keine Gerade der Schar
verläuft durch den Ur-
sprung.

Es gibt nur eine Gerade
der Schar, die die
x1-Achse schneidet.

 

Für a = —1 verläuft die
Gerade parallel zur
Xx1-X2-Ebene.

1 0
h) Gegeben ist die Ebene E, mit der Gleichung: E;: h _ (-)) . ®) =.
0 3
e Ermitteln Sie für die Ebene E, eine Ebenengleichung in Koordinatenform.

e Begründen Sie, dass die Ebene Ez:xz + x3 = 0 parallel zur Ebene E; ist.
Der Nachweis, dass die Ebenen nicht identisch sind, ist nicht gefordert.

Zentrale Abschlussprüfung Mathematik BG 20. März 2015
eAHT 15 SA1 und A2 AnaGeo OHNE CAS (Abschnitt 1) Seite 3 von 7

Punkteverteilung Aufgabe 2: Fun- und Kletterpark

Auiwenen | a [5 [oe Sales
meer || lol ale
Tr TR
Fr

Erstkorrektur
Zweitkorrektur

 

Der Tourismusverband in einem kleinen österreichischen Skigebiet plant für die
Sommergäste in Höhe der Mittelstation einen Fun- und Kletterpark zu errichten. Zunächst
soll eine Seilrutsche aufgebaut werden, die im Zick-Zack-Kurs von einer Talseite zur
anderen führt.

Der Chef des Tourismusverbandes hat bereits eine nicht maßstabsgetreue Skizze (Abb. 2.1)
erstellt, sowie einige Eckdaten ermitteln lassen. Alle Zahlenwerte sind in Metern
angegeben.

     

a — i i ; -P Alm-Hütte
u FT u nn tuehe un 5 i ea dr
N nme Felsplateaup "7 -TÖwer_S(-100/300/1510)
N IT 14 FERR — we" /
SINN NEE _ ET N 5 K;(-90/290/1500)

7 GE ra
(Wanderweg N

10250/1120) +

Ku

 

Abbildung 2.1: Entwurf einer Übersichtsskizze des Fun- und Kletterparks (nicht maßstäblich)

Zentrale Abschlussprüfung Mathematik BG 20. März 2015
eAHT 15 S Al und A2 AnaGeo OHNE CAS (Abschnitt 1) Seite4von 7

Aufgaben 1 und 2 eA Analytische Geometrie OHNE CAS Der Start-Tower soll in der Nähe der Alm-Hütte auf einem bereits vorhandenen Beton- fundament aufgebaut werden. Dorthin gelangt man nur über einen langen Wanderweg. Der Chef des Tourismusverbandes schlägt daher vor, einen Kletterstieg vom Punkt K[ (0|250|1420) als durchgehende, geradlinige Treppenkonstruktion (ohne Podeste) bis zum Punkt K J (−90|290|1500) unterhalb des Start-Towers zu errichten (Abb. 2.2). Abb. 2.2: Detailskizze des Kletterstiegs Abb. 2.3: Geplantes Hinweisschild am Kletterstieg a) Ermitteln Sie die fehlenden Angaben auf dem Hinweisschild (Abb. 2.3). In einem Umkreis von ca. 1,5 m um den Punkt K ` (−69|282|1481,5) lässt sich ein besonders schönes Echo erzeugen. b) Prüfen Sie, ob Gäste des Fun- und Kletterparks auf dem Kletterstieg die Möglichkeit haben dieses Echo zu erzeugen. Die Seilrutsche soll von der Spitze des Start-Towers S(−100|300|1510) in Richtung 1 USC UUUV = W−3X über den Change-Tower C im Zickzack-Kurs zum Landing-Tower L unterhalb −1 der Mittelstation führen. Für die Seilrutsche gilt aus Sicherheitsgründen, dass das Gefälle nicht mehr als 40 % gegenüber der Horizontalen betragen darf. c) Prüfen Sie, ob diese Sicherheitsbestimmung für den ersten Teil der Strecke vom Start- Tower S zum Change-Tower C eingehalten wird. Zentrale Abschlussprüfung Mathematik BG eA HT 15 S A1 und A2 AnaGeo OHNE CAS (Abschnitt 1) 20. März 2015 Seite 5 von 7

Aufgaben 1 und 2 eA Analytische Geometrie Der Start der Seilrutsche erfolgt von einer Rampe, die zwei Meter unterhalb der Spitze S am Start-Tower im Punkt A befestigt ist. Die Gäste nehmen in Richtung des Punktes R Anlauf. Damit beträgt die maximale Anlauflänge ca. zwei Meter. Die gestrichelt dargestellte Linie zwischen den Punkten A und R stellt die lotrechte Projektion des Seiles auf die Rampe dar. Gleichzeitig ist sie die Symmetrielinie der Rampe. Als weitere Eckpunkte sind E[ (−102,5|297,5|1506,75) und EJ (−96,5|299,5|1506,75) vorgesehen. OHNE CAS Abb. 2.4: Start-Tower mit Rampe Der TÜV hat jedoch die maximale Anlauflänge von nur ca. zwei Metern beanstandet und fordert stattdessen eine Verdoppelung der Anlauflänge. d) Zeigen Sie, dass die maximale Anlauflänge ca. zwei Meter beträgt. UUUUUUUV[ ), so Ermitteln Sie die Koordinaten des (in Verlängerung des Vektors AE dass die Forderung des TÜV auf Verdoppelung der Anlauflänge erfüllt wird. f Eckpunktes E[ Ursprünglichen Planungen zufolge sollte im Punkt F(300|525|1185) der Endpunkt des Seiles liegen. Der Chef des Tourismusverbandes möchte für den Fun- und Kletterpark aber unbedingt mit der längsten Seilrutsche Europas (mindestens 1,2 km) werben. Daher fordert er, dass die Seilrutsche zwischen dem Change-Tower C und dem Landing- Tower L über den Punkt F hinaus um ein Drittel länger wird, als sie zwischen dem Change- Tower C und dem Landing-Tower in F geworden wäre. Aufgrund der landschaftlichen Verhältnisse wird der Verlauf der Seilrutsche zwischen dem Change-Tower C und dem 4 UUUUV = W 7 X beschrieben. Landing-Tower L mit Hilfe des Vektors CL −3 e) Ermitteln Sie die Koordinaten der Spitze des Change-Towers und die Koordinaten der Spitze des Landing-Towers. Prüfen Sie, ob der Chef des Tourismusverbandes mit der längsten Seilrutsche Europas werben kann, wenn der erste Abschnitt zwischen Start- und Change-Tower ca. 332 Meter lang ist. Im mittleren Drittel des Abschnittes vom Start- zum Change- Tower verläuft die Seilrutsche nahe eines ansteigenden ebenen Felsplateaus (Abb. 2.5). Dieses Felsplateau P verläuft durch die Punkte P[ (−50|180|1360), PJ (−80|205|1420) und PB (−100|200|1470) Abb. 2.5: Detailskizze des Felsplateaus f) Stellen Sie die Normalenform der Ebenengleichung auf, die das Felsplateau beschreibt. Zeigen Sie, dass die Seilbahn im Abschnitt zwischen Start- und Change-Tower parallel zum Felsplateau verläuft. Zentrale Abschlussprüfung Mathematik BG eA HT 15 S A1 und A2 AnaGeo OHNE CAS (Abschnitt 1) 20. März 2015 Seite 6 von 7

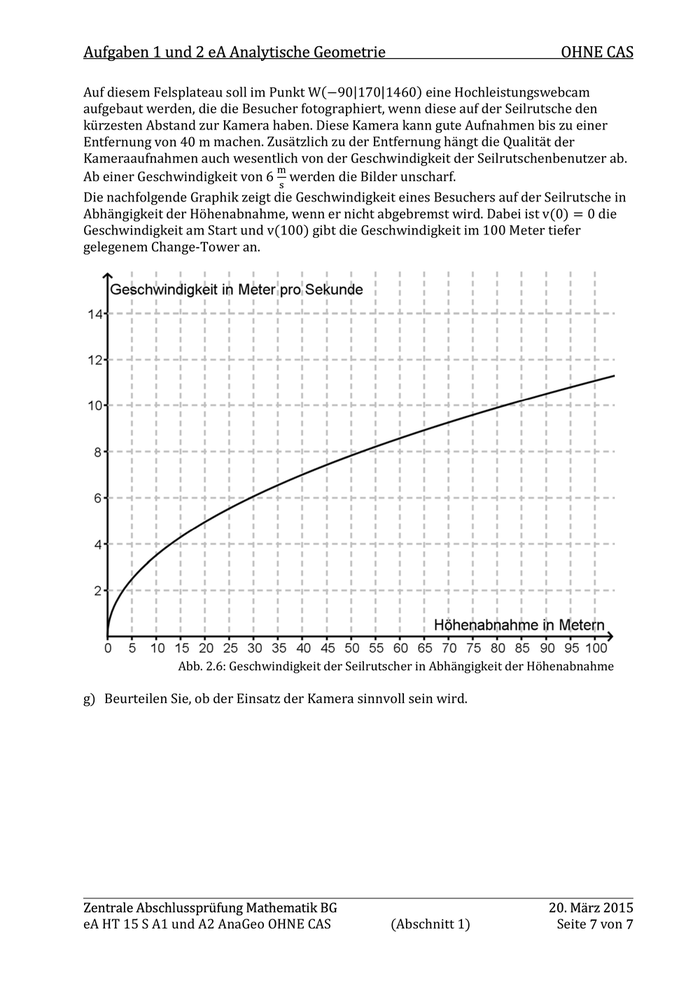
Aufgaben 1 und 2 eA Analytische Geometrie OHNE CAS Auf diesem Felsplateau soll im Punkt W(−90|170|1460) eine Hochleistungswebcam aufgebaut werden, die die Besucher fotographiert, wenn diese auf der Seilrutsche den kürzesten Abstand zur Kamera haben. Diese Kamera kann gute Aufnahmen bis zu einer Entfernung von 40 m machen. Zusätzlich zu der Entfernung hängt die Qualität der Kameraaufnahmen auch wesentlich von der Geschwindigkeit der Seilrutschenbenutzer ab. g Ab einer Geschwindigkeit von 6 h werden die Bilder unscharf. Die nachfolgende Graphik zeigt die Geschwindigkeit eines Besuchers auf der Seilrutsche in Abhängigkeit der Höhenabnahme, wenn er nicht abgebremst wird. Dabei ist v(0) = 0 die Geschwindigkeit am Start und v(100) gibt die Geschwindigkeit im 100 Meter tiefer gelegenem Change-Tower an. Abb. 2.6: Geschwindigkeit der Seilrutscher in Abhängigkeit der Höhenabnahme g) Beurteilen Sie, ob der Einsatz der Kamera sinnvoll sein wird. Zentrale Abschlussprüfung Mathematik BG eA HT 15 S A1 und A2 AnaGeo OHNE CAS (Abschnitt 1) 20. März 2015 Seite 7 von 7

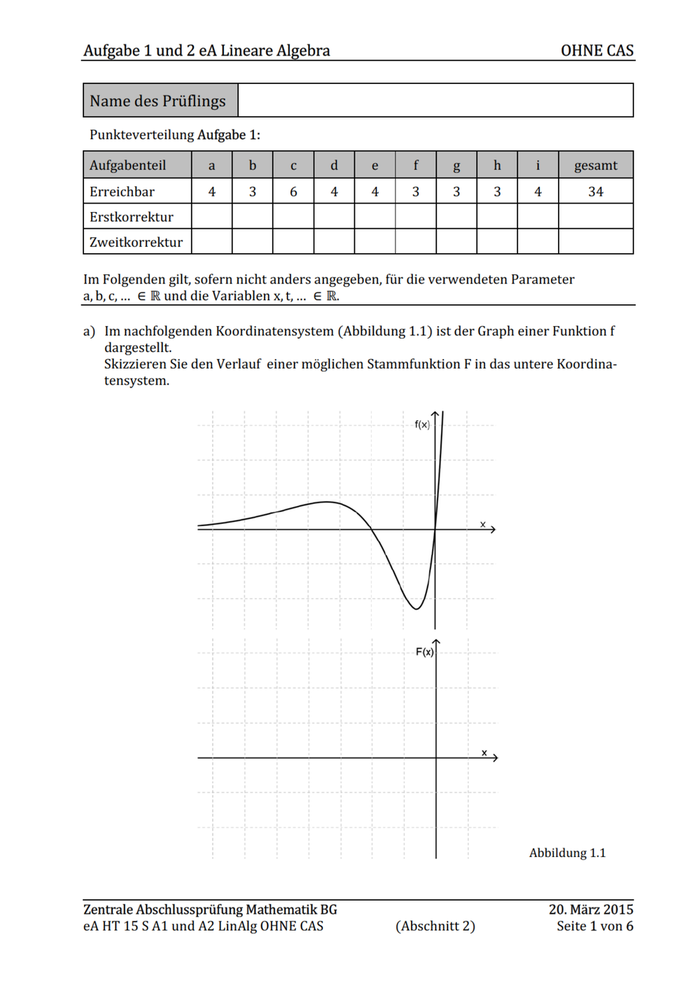
Aufgabe 1 und 2 eA Lineare Algebra OHNE CAS

Punkteverteilung Aufgabe 1:

 

Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter
a,b,c,... € Runddie Variablen x,t,... € R.

a) Im nachfolgenden Koordinatensystem (Abbildung 1.1) ist der Graph einer Funktion f
dargestellt.

Skizzieren Sie den Verlauf einer möglichen Stammfunktion F in das untere Koordina-

tensystem.
fix) |
Fix
x
Abbildung 1.1

Zentrale Abschlussprüfung Mathematik BG 20. März 2015
eAHT 15SA1 und A2 LinAlg OHNE CAS (Abschnitt 2) Seite 1 von 6

Aufgabe 1 und 2 eA Lineare Algebra OHNE CAS

b) Bestimmen Sie den Parameter a für die Funktion fa mit der Funktionsgleichung

3

f,x)=a'x®-x mita>0

so, dass der Graph der Funktion fa mit der x-Achse im IV. Quadranten einen
Flächeninhalt von 0,25 Flächeneinheiten (FE) einschließt.

c) Der Graph einer ganzrationalen Funktion f mit der allgemeinen Funktionsgleichung
f(x) =a’x*+b-x®+c:'x?+d:x+ e verläuft achsensymmetrisch zur Ordinatenachse,
hat im Punkt A(2]5) ein lokales Maximum und an der Stellex = —1 die Steigung
m=-—6.

Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind und begründen Sie.

Der zugehörige Funktionsterm
kann nicht eindeutig bestimmt
werden, da die Anzahl der ge-
gebenen Bedingungen zu ge-
ring ist.

Aus den gegebenen Bedingun-
gen lässt sich unter anderem
folgende Gleichung aufstellen:
d=0.

 

Um die Koeffizienten der
Funktion f bestimmen zu
können, wird die zweite
Ableitungsfunktion benötigt.

d) Gegeben ist die Funktion f} mit der Funktionsgleichung
f{(x) = cos(2(x+1)) +t.

Geben Sie an, für welche Werte des Parameters t der Graph innerhalb einer Periode die
Abszissenachse zweimal oder gar nicht schneidet.

Ermitteln Sie für t= 1 die Koordinaten der Berührpunkte mit der Abszissenachse in-
nerhalb des Intervalls [0; 2].

Zentrale Abschlussprüfung Mathematik BG 20. März 2015
eAHT 15SA1 und A2 LinAlg OHNE CAS (Abschnitt 2) Seite 2 von 6

Aufgabe 1 und 2 eA Lineare Algebra OHNE CAS

e) Formulieren Sie je eine Aussage über die Lösbarkeit der beiden folgenden linearen Glei-
chungssysteme und begründen Sie Ihre Aussage. (Eine explizite Lösung wird ausdrück-

lich nicht gefordert.)
3 2 -1 416
) e2) ( 32 ı
2

2 —I
el) ( -4 3
0 0 01-1 0 071

 

 

un j _f a b? _ (1 4
f) Gegeben sind die Matrizen A = (. Pe ) undB= ( > a

Bestimmen Sie die Matrix A so, dass 2A = Bggilt.

g) Ermitteln Sie eine mögliche Matrix X, für die die folgende Matrizengleichung gilt:
b\ _ a uv_ {11 Xı2
x

h) Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind.

Hinweis: Für jedes richtige Kreuz gibt es einen Punkt, für jedes falsche Kreuz gibt
es null Punkte, nicht angekreuzte Zeilen bleiben neutral (null Punkte).

Jede Matrix hat eine zugehörige inverse Matrix.

Wenn die quadratischen Matrizen A und B vom gleichen Typ sind,
dann gilt: (A- B=t)T = (B!)T. AT,

Hat die Matrizengleichung: M -x = X einen von Null verschiedenen
Lösungsvektor x, so ist der Vektor X Fixvektor zur Matrix M.

 

i) Ermitteln Sie die Matrix X in der Matrizengleichung A -X+ B = A mit den Matrizen

1
sa a
A=(, 0) und B = . i ‚aD,
2a a a Sa
2 2
Zentrale Abschlussprüfung Mathematik BG 20. März 2015

eAHT 15SA1 und A2 LinAlg OHNE CAS (Abschnitt 2) Seite 3 von 6