Mathematik_BG_gA_HT_2016_geschwrzt.pdf
Dieses Dokument ist Teil der Anfrage „BG Abiturklausuren 2013-2019 SH“
Aufgaben 1 und 2 Analytische Geometrie gA Name des Prüflings Zetuniedermn ) Aufgaben [a Ivo Tefalefr ereichbr | 5 | 5 | 5 | 5 | 5 5 | EEE HE EEE EEE HE KEEE E (Zweitkorrenme |) | [| Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter: Punkteverteilung Aufgabe 1: a,b,c,... € Runddie Variablen: x,t,... ER. a) Gegeben ist die Gleichung der abschnittsweise definierten Funktion f mit: _$1,5x?—-5x+3 fürx<s3 19 =| 4x+b fürx>3' Der Graph der Funktion f hat im Intervall I mit I = [1; 2] keine Nullstellen. al) Bestimmen Sie die Gleichung der 1. Ableitung der Funktion f. a2) Bestimmen Sie den Koeffizienten b so, dass der Graph f sprung- und knickfrei verläuft. a3) Berechnen Sie den Wert des folgenden Integrals: [ E f(x) dx und geben Sie die Bedeutung dieses Wertes an. b) Entscheiden Sie ausgehend von der Funktion f mit der Gleichung: fx) = a: sin(b-(x-c))+dmita,b # 0, ob die folgenden Aussagen wahr oder falsch sind. Hinweis: Für jedes richtige Kreuz gibt es einen Punkt, für jedes falsche Kreuz gibt es null Punkte, nicht angekreuzte Zeilen bleiben neutral (null Punkte). Der Wert des Parameters a ist generell doppelt so hoch wie der Wert des Parameters d. Wenna=b=1undc=d = Ogilt, so befindet sich eine maximale, positive Änderungsrate beix = n. Wenna=b=1undc=d = Ogilt, beträgt der Integralwert über eine Periodenlänge der Funktion f null. Füra=3,b=2undc=d = Ogilt: Die Periodenlänge beträgt p = 2n. Fürb = 1und c = O beschreiben die Gleichungen der Funktionen f =) + d den gleichen Funktions- und gmitg(x) = a cos (b . (x _ sraphen. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 gAHT 16 S Al und A2 AnaGeo (Abschnitt 1) Seite1von5
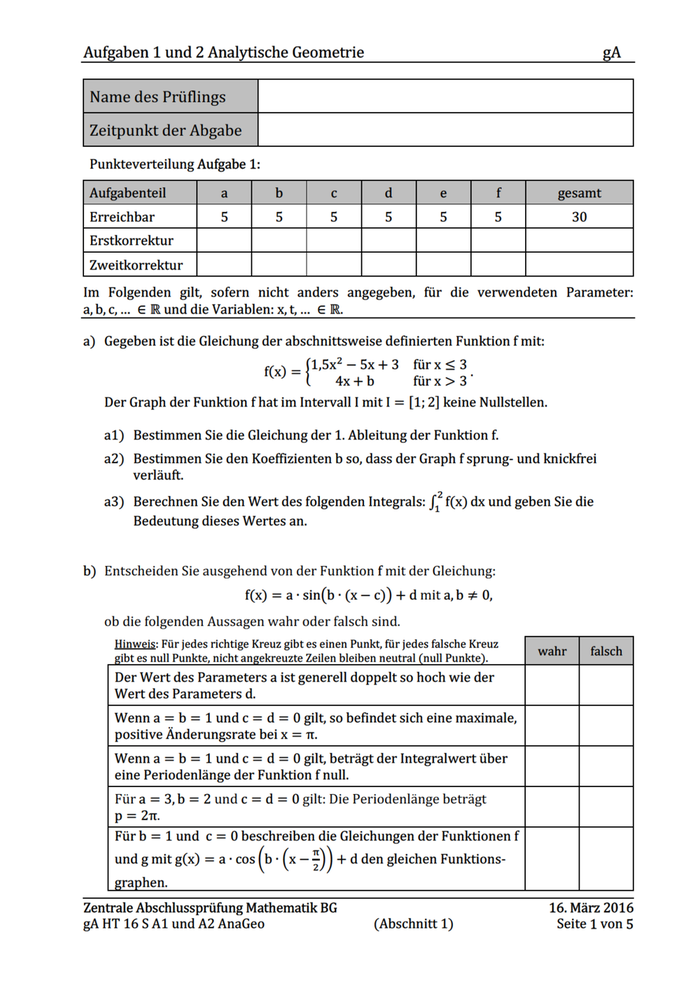
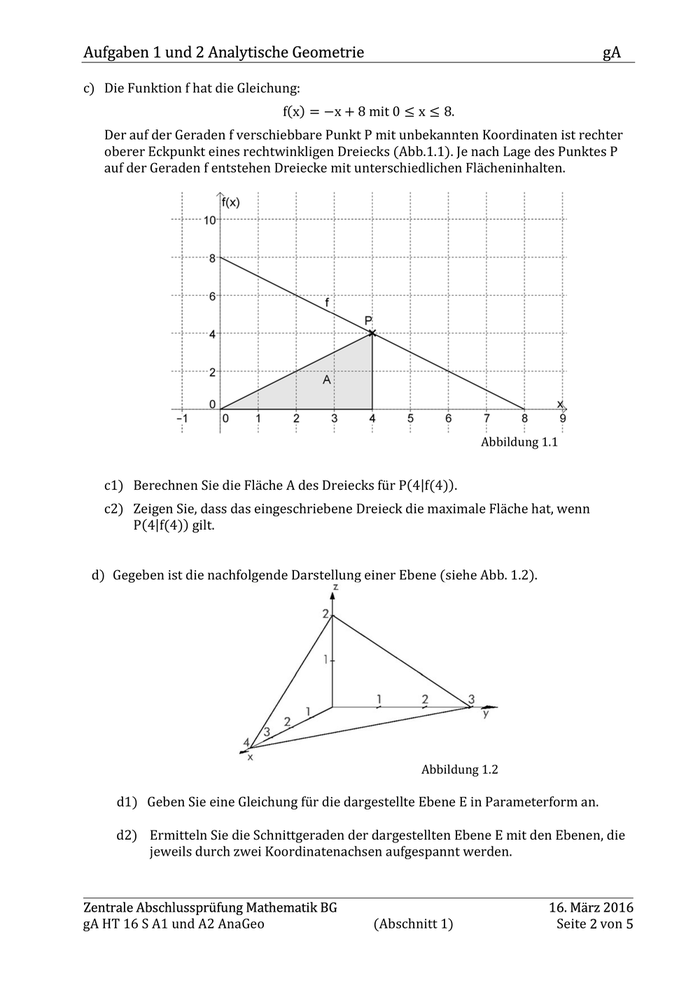
Aufgaben 1 und 2 Analytische Geometrie gA c) Die Funktion f hat die Gleichung: f(x) = −x + 8 mit 0 ≤ x ≤ 8. Der auf der Geraden f verschiebbare Punkt P mit unbekannten Koordinaten ist rechter oberer Eckpunkt eines rechtwinkligen Dreiecks (Abb.1.1). Je nach Lage des Punktes P auf der Geraden f entstehen Dreiecke mit unterschiedlichen Flächeninhalten. c1) Berechnen Sie die Fläche A des Dreiecks für P(4|f(4)). Abbildung 1.1 c2) Zeigen Sie, dass das eingeschriebene Dreieck die maximale Fläche hat, wenn P(4|f(4)) gilt. d) Gegeben ist die nachfolgende Darstellung einer Ebene (siehe Abb. 1.2). Abbildung 1.2 d1) Geben Sie eine Gleichung für die dargestellte Ebene E in Parameterform an. d2) Ermitteln Sie die Schnittgeraden der dargestellten Ebene E mit den Ebenen, die jeweils durch zwei Koordinatenachsen aufgespannt werden. Zentrale Abschlussprüfung Mathematik BG gA HT 16 S A1 und A2 AnaGeo (Abschnitt 1) 16. März 2016 Seite 2 von 5
Aufgaben 1 und 2 Analytische Geometrie gA e) Gegeben sind die Gleichungen der folgenden drei Geraden in der Parameterdarstellung: 2 1 gH : YxZ= [2\ + rH ∙ [1\, 1 2 4 g : : YxZ= r: ∙ [4\ 2 und 1 2 g ] : YxZ= [2\ + r] ∙ [2\. 4 4 e1) Zeigen Sie, dass der Stützvektor der Geraden g ] nicht auf der Geraden g : liegt. e2) Zeigen Sie, dass die Geraden gH und g ] parallel zueinander verlaufen, aber nicht identisch sind. e3) Berechnen Sie den Schnittpunkt der Geraden gH und g : . f) Gegeben sind die Ebenen EH und E: mit den Gleichungen: −6 2 0,5 EH : 4x + 2y + 4z = 20 und E: : YxZ = [ 0 \ + s [ 0 \ + t [−1\. 0 −2 0 −4 Der Vektor YnYYYYYZ ^_ = `−2a ist ein Normalenvektor der Ebene E: . −4 f1) Geben Sie eine Gleichung der Ebene EH in der Parameterform an. f2) Zeigen Sie, dass die Normalenvektoren der Ebenen EHund E: linear abhängig sind. Zentrale Abschlussprüfung Mathematik BG gA HT 16 S A1 und A2 AnaGeo (Abschnitt 1) 16. März 2016 Seite 3 von 5

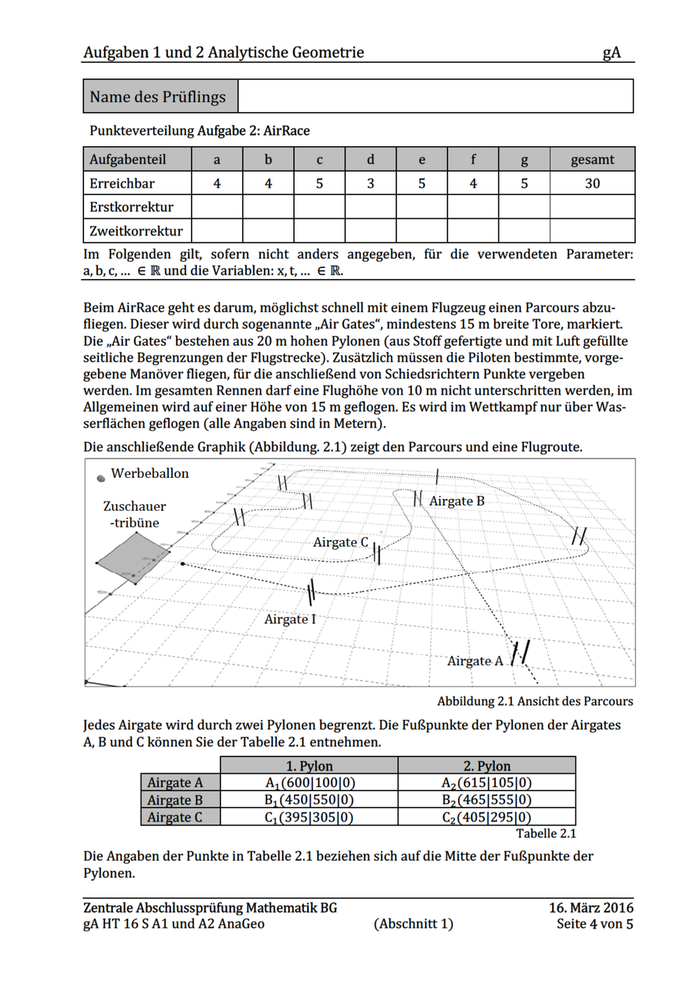
Aufgaben 1 und 2 Analytische Geometrie gA Punkteverteilung Aufgabe 2: AirRace Aufgabenteil Zweiioraam | | RP PTR Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter: a,b,c,... € Rund die Variablen: x,t,... € R. Beim AirRace geht es darum, möglichst schnell mit einem Flugzeug einen Parcours abzu- fliegen. Dieser wird durch sogenannte „Air Gates“, mindestens 15 m breite Tore, markiert. Die „Air Gates“ bestehen aus 20 m hohen Pylonen (aus Stoff gefertigte und mit Luft gefüllte seitliche Begrenzungen der Flugstrecke). Zusätzlich müssen die Piloten bestimmte, vorge- gebene Manöver fliegen, für die anschließend von Schiedsrichtern Punkte vergeben werden. Im gesamten Rennen darf eine Flughöhe von 10 m nicht unterschritten werden, im Allgemeinen wird auf einer Höhe von 15 m geflogen. Es wird im Wettkampf nur über Was- serflächen geflogen (alle Angaben sind in Metern). Die anschließende Graphik (Abbildung. 2.1) zeigt den Parcours und eine Flugroute. o Werbeballon - ge F---- we Zuschauer . aM \ N Airgate B -tribüne > “ Airgate I Airgate A / / Abbildung 2.1 Ansicht des Parcours Jedes Airgate wird durch zwei Pylonen begrenzt. Die Fußpunkte der Pylonen der Airgates A,B und C können Sie der Tabelle 2.1 entnehmen. 1.Pylon | 2.Pyon | A, (600|100]0 A,(615|105]0 B, (450]550]0 B,(465|555|0 C,(395|305]0 C,(405|295]0 Tabelle 2.1 Die Angaben der Punkte in Tabelle 2.1 beziehen sich auf die Mitte der Fußpunkte der Pylonen. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 gAHT 16 S Al und A2 AnaGeo (Abschnitt 1) Seite 4von5
Aufgaben 1 und 2 Analytische Geometrie Als erste Aufgabe sind vom Piloten nacheinander die Airgates A und B zu durchfliegen. Dafür darf er nicht länger als 5 Sekunden benötigen. gA a) Begründen Sie, dass sich die entsprechende Flugroute mit der folgenden Gleichung 607,5 −150 h: YxZ = [ 102,5\ + r ∙ [ 450 \ 15 0 beschreiben lässt, wenn davon ausgegangen wird, dass die Airgates mittig zwischen den Pylonen durchflogen werden. b) Ermitteln Sie die Geschwindigkeit in Kilometer pro Stunde, mit der der Pilot mindes- tens fliegen muss, um diese erste Aufgabe zu erfüllen. Im Anschluss daran absolviert der Pilot einen Steigflug mit mehreren Pirouetten (nicht in Abbildung 2.1 dargestellt). Nach Abschluss dieser Manöver befindet er sich im Punkt P(800|700|300). Von hier aus muss er das Airgate C auf einer Höhe von 15 m passieren. −80 Dazu fliegt er in Richtung des Vektors: v YZ = [−80\. −57 c) Weisen Sie rechnerisch nach, dass der Pilot das Airgate C auf einer Höhe von 15 m passiert. Der Pilot kann den Sinkflug bei einer solchen Höhe nur dann abfangen, wenn der Schnitt- winkel in dieser Situation gegenüber der Wasseroberfläche beim Passieren des Airgates nicht größer als 30° ist. (Die Wasseroberfläche wird in diesem Fall als plane Fläche mit der Höhe z = 0 betrachtet.) d) Prüfen Sie, ob der Pilot die Maschine noch rechtzeitig abfangen kann. Die Zuschauertribüne lässt sich durch die Koordinaten der Eckpunkte TH (20|180|0), T: (10|280|0), T3(−40|275|40) und Tk (−30|175|40) beschreiben (siehe Abb. 2.1). e) Begründen Sie, dass die Ebene E mit der Ebenengleichung −50 10 10 E: YxZ = `280a + s ∙ `−100a + t ∙ [ −5 \ mit 0 ≤ s ≤ 1 und 0 ≤ t ≤ 1 0 0 40 die Zuschauertribüne beschreibt. f) Ermitteln Sie die Zuschauerkapazität der Tribüne unter der Maßgabe, dass pro Sitz- platz 0,75 m² berücksichtigt und 20% der Gesamtfläche für Aufgänge benötigt werden. Zum Abschluss durchfliegt der Pilot mittig das Airgate I im Punkt I(320|177,5|15) und fliegt dann zum Abschied in Richtung des Punktes Q(100|200|35) und somit in Richtung der Zuschauertribüne. g) Prüfen Sie, ob es bei dem gegenwärtigen Kurs zu einer Kollision mit der Zuschauer- tribüne kommen könnte, wenn der Schnittpunkt der Fluggeraden und der Tribünen- ebene im Punkt Po (−44,32|214,76|48,12) liegt. Zentrale Abschlussprüfung Mathematik BG gA HT 16 S A1 und A2 AnaGeo (Abschnitt 1) 16. März 2016 Seite 5 von 5

Aufgaben 1 und 2 Lineare Algebra gA Name des Prüflings Zeitpunkt der Abgabe Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter: a,b,c,... € Runddie Variablen: x,t,... ER. a) Gegeben ist die Gleichung der abschnittsweise definierten Funktion f mit: _$1,5x?-5x+3 fürx<3 19 =| 4x+b fürx>3' Der Graph der Funktion f hat im Intervall I mit I = [1; 2] keine Nullstellen. al) Bestimmen Sie die Gleichung der 1. Ableitung der Funktion f. a2) Bestimmen Sie den Koeffizienten b so, dass der Graph f sprung- und knickfrei verläuft. a3) Berechnen Sie den Wert des folgenden Integrals: £ f(x) dx und geben Sie die Bedeutung dieses Wertes an. b) Entscheiden Sie ausgehend von der Funktion f mit der Gleichung: fx) =a- sin(b (x-— c)) +dmita,b #0, ob die folgenden Aussagen wahr oder falsch sind. Hinweis: Für jedes richtige Kreuz gibt es einen Punkt, für jedes falsche Kreuz gibt es null Punkte, nicht angekreuzte Zeilen bleiben neutral (null Punkte). Der Wert des Parameters a ist generell doppelt so hoch wie der Wert des Parameters d. Wenna=b=1undc=d = Ogilt, so befindet sich eine maximale, positive Änderungsrate beix = n. Wenna=b=1undc=d = Ogilt, beträgt der Integralwert über eine Periodenlänge der Funktion f null. Füra=3,b=2undc=d = Ogilt: Die Periodenlänge beträgt p = 2. Fürb = 1und c = O beschreiben die Gleichungen der Funktionen f und gmitg(x) = a: cos (b i (x _ =)) + d den gleichen Funktions- sraphen. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 gAHT 16S Al und A2 LinAlg (Abschnitt 2) Seite 1von 6
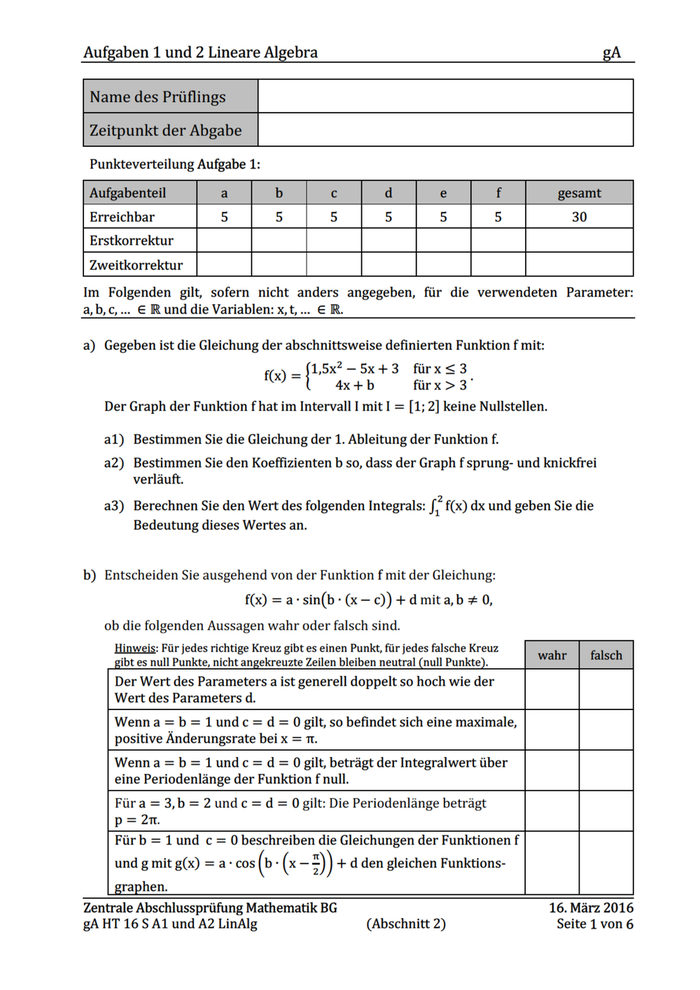
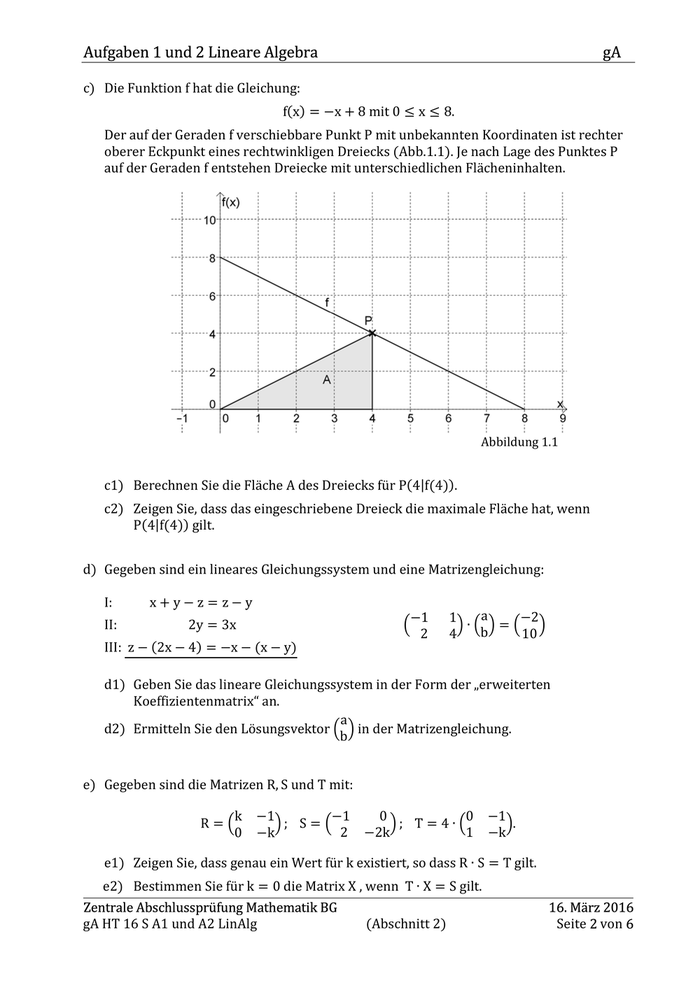
Aufgaben 1 und 2 Lineare Algebra gA c) Die Funktion f hat die Gleichung: f(x) = −x + 8 mit 0 ≤ x ≤ 8. Der auf der Geraden f verschiebbare Punkt P mit unbekannten Koordinaten ist rechter oberer Eckpunkt eines rechtwinkligen Dreiecks (Abb.1.1). Je nach Lage des Punktes P auf der Geraden f entstehen Dreiecke mit unterschiedlichen Flächeninhalten. c1) Berechnen Sie die Fläche A des Dreiecks für P(4|f(4)). Abbildung 1.1 c2) Zeigen Sie, dass das eingeschriebene Dreieck die maximale Fläche hat, wenn P(4|f(4)) gilt. d) Gegeben sind ein lineares Gleichungssystem und eine Matrizengleichung: I: II: x+y−z= z−y 2y = 3x III: z − (2x − 4) = −x − (x − y) −1 Q 2 a −2 1 S∙Q S=Q S b 10 4 d1) Geben Sie das lineare Gleichungssystem in der Form der „erweiterten Koeffizientenmatrix“ an. a d2) Ermitteln Sie den Lösungsvektor Q S in der Matrizengleichung. b e) Gegeben sind die Matrizen R, S und T mit: k R=Q 0 −1 −1 0 0 −1 S; S = Q S; T = 4 ∙ Q S. 2 −2k 1 −k −k e1) Zeigen Sie, dass genau ein Wert für k existiert, so dass R ∙ S = T gilt. e2) Bestimmen Sie für k = 0 die Matrix X , wenn T ∙ X = S gilt. Zentrale Abschlussprüfung Mathematik BG gA HT 16 S A1 und A2 LinAlg (Abschnitt 2) 16. März 2016 Seite 2 von 6
Aufgaben 1 und 2 Lineare Algebra f) Gegeben sind die folgenden Matrizen: A=(7 ,). B=(_) Bu c=() 0) und D=(° =) Entscheiden Sie, welche der folgenden Aussagen wahr bzw. falsch sind. Hinweis: Für jedes richtige Kreuz gibt es einen Punkt, für jedes falsche Kreuz gibt es null Punkte, nicht angekreuzte Zeilen bleiben neutral (null Punkte). Für die Matrix D gilt: D = AT. Die Rechenoperation A - B -— B ist definiert. Zur Matrix C existiert keine inverse Matrix. Es gilt: c?? =Emitne Nundn > 1, wobei die Matrix E die Einheits- matrix ist. Die Matrix M, für dieM = B: Bggilt, ist vom gleichen Typ wie die Matrix B. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 gAHT 16S Al und A2 LinAlg (Abschnitt 2) Seite 3 von 6

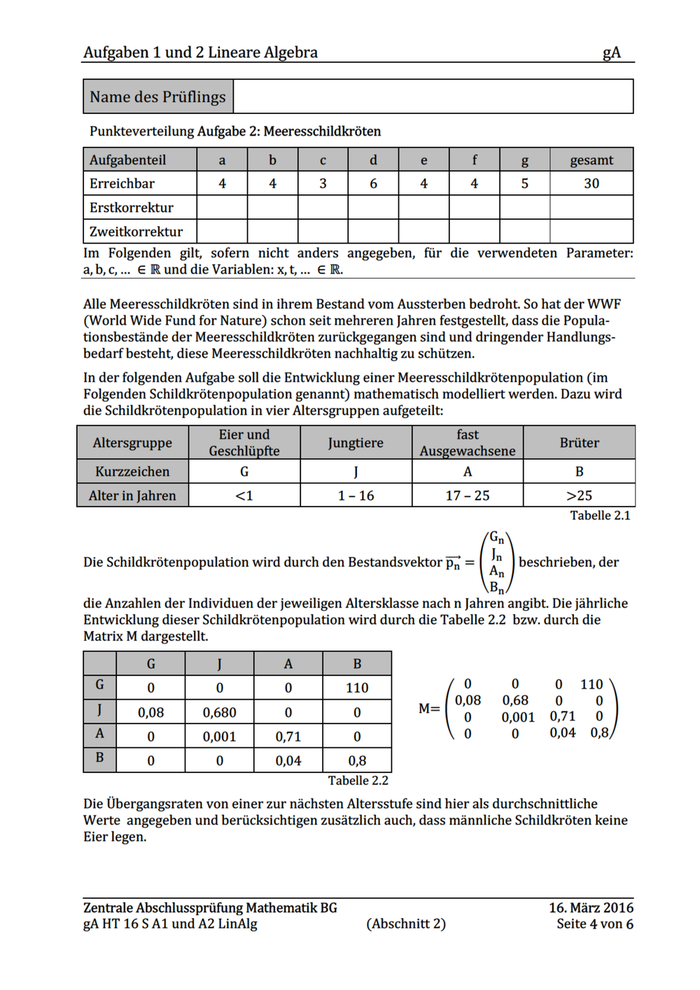
Aufgaben 1 und 2 Lineare Algebra gA Punkteverteilung Aufgabe 2: Meeresschildkröten EEE En EEE meiner | ala |a|o|a|la|s| w | (zweite | | [ [ jJ p Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter: a,b,c,... € Runddie Variablen: x,t,... ER. Alle Meeresschildkröten sind in ihrem Bestand vom Aussterben bedroht. So hat der WWF (World Wide Fund for Nature) schon seit mehreren Jahren festgestellt, dass die Popula- tionsbestände der Meeresschildkröten zurückgegangen sind und dringender Handlungs- bedarf besteht, diese Meeresschildkröten nachhaltig zu schützen. In der folgenden Aufgabe soll die Entwicklung einer Meeresschildkrötenpopulation (im Folgenden Schildkrötenpopulation genannt) mathematisch modelliert werden. Dazu wird die Schildkrötenpopulation in vier Altersgruppen aufgeteilt: Eier und : fast Altersgruppe | geschtüpne | Jungtiere [Jusgemachsene| Brüter Kurzeichen | Oo 6 | | Alter in Jahren 17-25 Tabelle 2.1 Gn Die Schildkrötenpopulation wird durch den Bestandsvektor p, = ae beschrieben, der n Bn die Anzahlen der Individuen der jeweiligen Altersklasse nach n Jahren angibt. Die jährliche Entwicklung dieser Schildkrötenpopulation wird durch die Tabelle 2.2 bzw. durch die Matrix M dargestellt. 0 0 0 110 0,08 0,68 0 0 0 0,001 0,71 0 0 0 0,04 0,8 Tabelle 2.2 Die Übergangsraten von einer zur nächsten Altersstufe sind hier als durchschnittliche Werte angegeben und berücksichtigen zusätzlich auch, dass männliche Schildkröten keine Eier legen. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 gAHT 16S Al und A2 LinAlg (Abschnitt 2) Seite 4 von 6
Aufgaben 1 und 2 Lineare Algebra a) Erstellen Sie einen Übergangsgraphen für die in der Matrix M bzw. in der Tabelle 2.2 angegebenen Informationen anhand der Abbildung 2.1. el LI 2] Gl Abbildung 2.1 b) Erläutern Sie die Bedeutung der von Null verschiedenen Elemente auf der Hauptdiago- nalen der Matrix M und die Bedeutung des Matrixelementes m3, = 0,001. c) Begründen Sie allgemein und im Sachzusammenhang, dass die Matrix M keine stochastische Matrix ist. Der WWF hat unter anderem festgestellt, dass z. B. die Population der Lederschildkröte im Ostpazifik in den letzten 20 Jahren um 90 % zurückgegangen ist. Deshalb beobachtet ein Forscherteam die Schildkrötenpopulation nun besonders intensiv und kann durch ihre Beobachtungen einen Schildkrötenpopulationsbestand feststellen, der 14 000 mit Hilfe des Bestandsvektors p, = : = beschrieben wird. 130 d) Berechnen Sie mit Hilfe der Modellierung durch die Matrix M jeweils den Bestands- vektor der Schildkrötenpopulation nach einem, nach fünf und nach neun Jahren. Vergleichen Sie die zukünftige Entwicklung dieser gesamten Schildkrötenpopulation seit Beobachtungsbeginn mit der Entwicklung der Population der Lederschildkröte im Ostpazifik in den letzten 20 Jahren. Zu Beginn einer intensiven zweijährigen Untersuchung der Schildkrötenpopulation ließen statistische Erhebungen erkennen, dass es doppelt so viele Jungtiere (J) wie fast Ausge- wachsene (A) gab. Von der Anzahl der Eier und der Geschlüpften (G) wird angenommen, dass sie dreimal so groß ist wie die der fast Ausgewachsenen (A). Die Zahl der Brüter (B) wird auf 10 % der fast Ausgewachsenen (A) geschätzt. e) Bestimmen Sie die Verteilung der Schildkrötenpopulation auf die einzelnen Altersgrup- pen zu Beginn der Untersuchung, wenn insgesamt von einem Bestand von 24 400 Indi- viduen dieser Schildkrötenpopulation ausgegangen wird. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 gAHT 16S Al und A2 LinAlg (Abschnitt 2) Seite 5 von 6










