Mecklenburg-Vorpommern Zentralabitur 2013 Mathematik ohne CAS Aufgaben

Abitur 2013 Mathematik ohne CAS                                                       Seite 2 Hinweise für Schüler Aufgabenwahl:              Die Prüfungsarbeit besteht aus den Teilen A und B. Der Teil A ist von allen Prüfungsteilnehmern zu bearbeiten. Von den Aufgaben A1, A2 und A3 sind zwei auszuwählen. Prüfungsteilnehmer, die die Prüfung unter erhöhten Anforderungen ablegen, bearbeiten zusätzlich den Prüfungsteil B. Von den Aufgaben Biund B2ist eine auszuwählen. Bearbeitungszeit:         Allen Prüfungsteilnehmernsteht eine Bearbeitungszeit von 195 Minuten zuzüglich 30 Minuten für die Aufgabenauswahl zur Verfügung. Den Prüfungsteilnehmern, die die Prüfung unter erhöhten Anforderungenablegen, stehen zusätzlich 60 Minuten Bearbeitungszeit zur Verfügung. Hilfsmittel:               Für die Bearbeitung der Aufgaben sind zugelassen: °   das an der Schule eingeführte Tafelwerk, °   deran der Schule zugelassene Taschenrechner ohne CAS, e   Zeichengeräte, °   ein Wörterbuch der deutschen Rechtschreibung. (Schülerinnen und Schüler, deren Muttersprachenicht die deutsche Sprache ist, könnenals zusätzliches Hilfsmittel ein zweisprachiges Wörterbuchin gedruckter Form verwenden. Näheres regelt die Schule.) Hinweis:                   Die Lösungen sindin einer sprachlich korrekten, mathematisch exakten und äußerlich einwandfreien Form darzustellen. In der Niederschrift müssen die Lösungswege nachvollziehbar sein. Entwürfe können ergänzend zur Bewertung nur herangezogen werden, wenn sie zusammenhängend konzipiert sind und die Reinschrift etwa drei Viertel des zu erreichenden Gesamtumfanges beinhaltet. Sonstiges:                 Maximal zwei Bewertungseinheiten können zusätzlich vergeben werden bei °    guter Notation und Darstellung, °    eleganten, kreativen und rationellen Lösungswegen, °    vollständiger Lösungeiner zusätzlichen Wahlaufgabe. Maximal zwei Bewertungseinheiten können bei mehrfachen Formverstößen abgezogen werden.

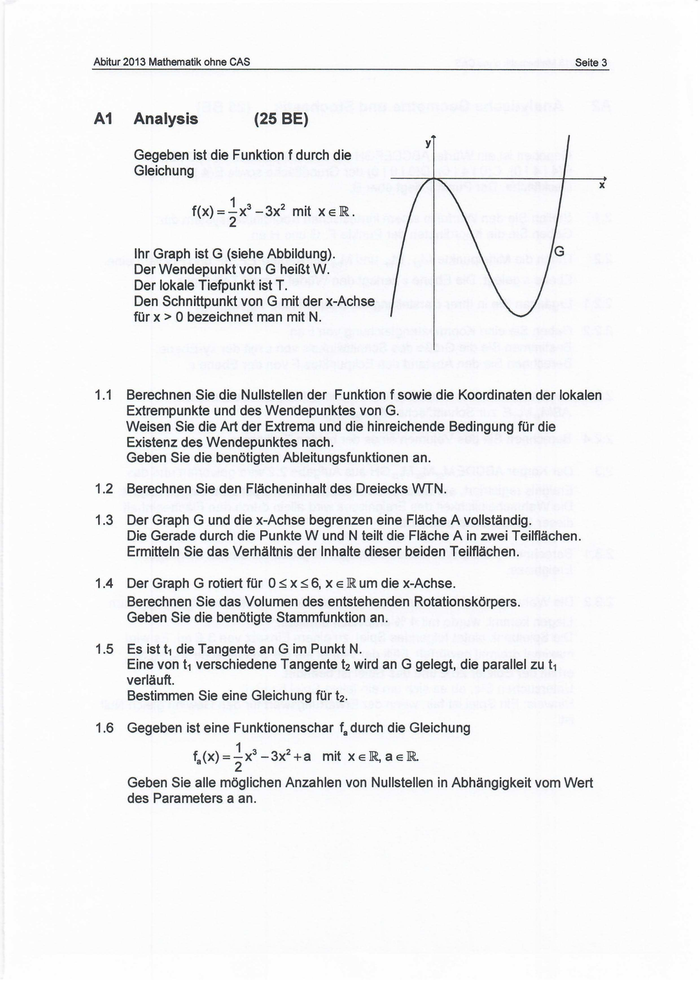
Abitur 2013 Mathematik ohne CAS                                                   Seite 3 A1       Analysis               (25 BE) yt Gegebenist die Funktion f durch die Gleichung                                                                      , x f(x) = 5x -3x? mit xeR. Ihr Graphist G (siehe Abbildung).                                     G Der Wendepunkt von G heißt W. Derlokale Tiefpunktist T. Den Schnittpunkt von G mit der x-Achse für x > 0 bezeichnet man mit N. 1.1     Berechnen Sie die Nullstellen der Funktion f sowie die Koordinaten der lokalen Extrempunkte und des Wendepunktes von G. Weisen Sie die Art der Extrema und die hinreichende Bedingung für die Existenz des Wendepunktes nach. GebenSie die benötigten Ableitungsfunktionen an. 1.2     BerechnenSie den Flächeninhalt des Dreiecks WTN. 1.3    Der Graph G unddie x-Achse begrenzen eine Fläche A vollständig. Die Gerade durch die Punkte W und N teilt die Fläche A in zwei Teilflächen. Ermitteln Sie das Verhältnis der Inhalte dieser beiden Teilflächen. 1.4    Der Graph G rotiert für O<x<6, xe Rum die x-Achse. Berechnen Sie das Volumen des entstehenden Rotationskörpers. Geben Sie die benötigte Stammfunktion an. 1.5    Es ist tı die Tangente an G im Punkt N. Eine von tı verschiedene Tangentet, wird an G gelegt, die parallel zu tı verläuft. Bestimmen Sie eine Gleichungfür tz. 1.6    Gegebenist eine Funktionenschar f, durch die Gleichung 9 =5x -3x?+a mit xeRaeR. GebenSie alle möglichen Anzahlen von Nullstellen in Abhängigkeit vom Wert des Parameters a an.

Abitur 2013 Mathematik ohne CAS                                                    Seite 4 A2         Analytische Geometrie und Stochastik                  (25 BE) Gegebenist ein Würfel ABCDEFGH mit den Eckpunkten A(4 | 0 | 0), B(4|4|0), C(0]4| 0), D(0 | 0 | 0) der Grundfläche sowie E(4 | 0 | 4) der Deckfläche. Der Punkt F liegt über B. 2.1      Stellen Sie den Würfel in einem kartesischen Koordinatensystem dar. Geben Sie die Koordinaten der Punkte F, Gund Han. 2.2      Durch die Mittelpunkte M,;,, M,, und M., der Kanten EF, BF und FG wird eine Ebene e gelegt. Die Ebene e zerlegt den Würfel in zwei Teilkörper. 2.2.1    Ergänzen Sie in Ihrer Darstellung die Schnittfläche M;-M,-M.... 2.2.2 GebenSie eine Koordinatengleichung von & an. Bestimmen Sie die Größe des Schnittwinkels von e mit der xy-Ebene. BerechnenSie den Abstand des Eckpunktes F von der Ebenee. 2.2.3 Bestimmen Sie das Verhältnis der Flächeninhalte der Seitenfläche ABM,-M;-E zur Schnittfläche M.-M;-M.. . 2.2.4 Berechnen Sie das Volumeneinesder beiden Teilkörper. 2.3      Der Körper ABCDE M..M,-M-.. GH aus Aufgabe 2.2 wird geworfen und das Ereignis registriert, auf welcher Seitenfläche der Körper zum Liegen kommt. Die Wahrscheinlichkeit des Ereignisses wird allein durch den Flächeninhalt dieser Seitenfläche bestimmt. 2.3.1 BerechnenSie die Wahrscheinlichkeiten für jedes der sieben möglichen Ereignisse. 2.3.2 Die Wahrscheinlichkeit, dass der Würfel auf der Seitenfläche M,-M,-M.. zum Liegen kommt, wurde mit 4 % empirisch ermittelt. Die Spielbank bietet folgendes Spiel zu einem Einsatz von 3 € an. Es wird maximal dreimal gewürfelt. Fällt der Würfel auf die Seitenfläche M.-M,-M.. erhält der Spieler 20 € und dasSpiel ist beendet. Untersuchen Sie, ob es sich um ein faires Spiel handelt. Hinweis: Ein Spiel ist fair, wenn der Erwartungswert für den Gewinn gleich Null ist.

Abitur 2013 Mathematik ohne CAS                                                    Seite 5 A3 Analysis                     (25 BE) Gegebensind die Funktionen f und g                          Kı durch die Gleichungen 3 t9= + =x+- mit xeD, und x         x                                                         K, 1     UM: g(x)   ze X)=—X+—        mit xeR. Der Graph von ist Kı und der vong ist K..                                          %                                      x 3.1    Geben Sie den Definitionsbereich vonf an. UntersuchenSie das Verhalten von K; im Unendlichen. BerechnenSie die Nullstelle von f und die Koordinaten des Extrempunktes von Kı. WeisenSie die Art des Extremumsnach. Begründen Sie, dass K; keine Wendepunktebesitzt. GebenSie die Gleichungen der benötigten Ableitungsfunktionen an. 3.2    Ermitteln Sie die Größe des Winkels, den die Tangente an K; im Punkt R(1 | f(1)) mit der x-Achsebildet. 3.3 Weisen Sie nach, dass die Graphen einanderan den Stellen xı = 1undx=2 schneiden. Kı und K; schließen eine Fläche vollständig ein. BerechnenSie den Inhalt dieser Fläche. GebenSie die Gleichung der benötigten Stammfunktion an. 3.4    Der Punkt P(u | v) mit u >   0 liegt auf K.. Die Parallele zur x-Achse    durch den Punkt P schneidet die y-Achse im PunktA. Die Parallele zur y-Achse    durch den Punkt P schneidet die x-Achse im Punkt B. Der Koordinatenursprung      O sowie die Punkte A und B sind Eckpunkte eines Dreiecks. Ermitteln Sie den Wert von u so, dass der Flächeninhalt des Dreiecks OAB extremal wird. Weisen Sie die Art des Extremums nach. 3.5    Im Folgenden wird zusätzlich die Funktionenschar h, mit der Gleichung h,(x)=-x?+x+a mitxeRaeR betrachtet. Kı und der Graph von h, berühren einanderin zwei Punkten. BerechnenSie die Koordinaten dieser Berührungspunkte. Geben Sie den zugehörigen Wert für a an. Hinweis: In einem Berührungspunkt habendie beiden Graphendengleichen Anstieg.

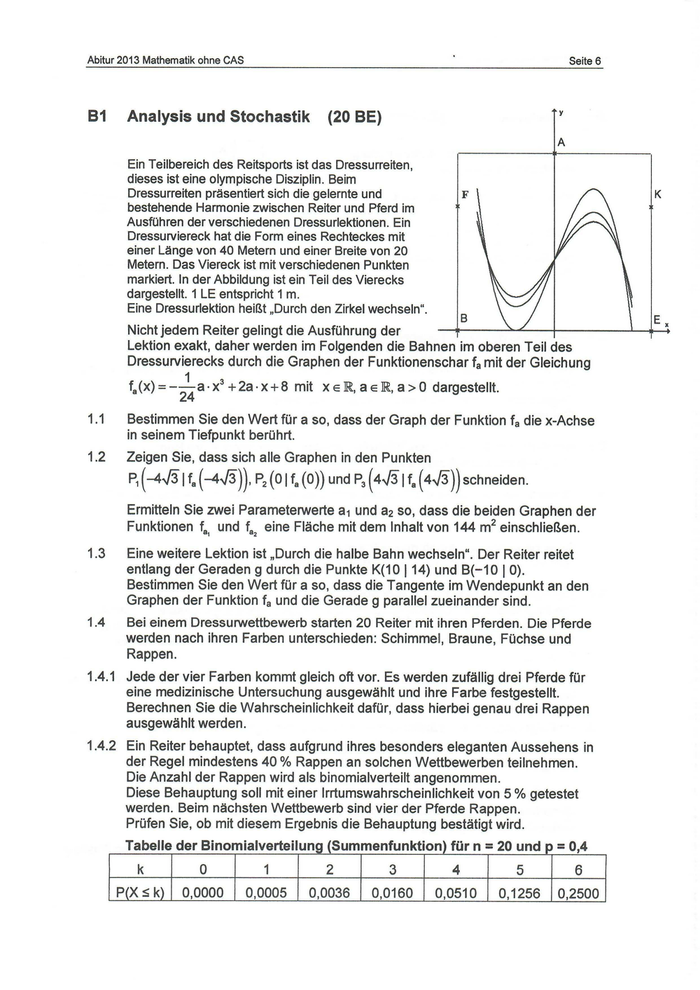
Abitur 2013 Mathematik ohne CAS                                                     Seite 6 B1       Analysis und Stochastik               (20 BE) Ein Teilbereich des Reitsports ist das Dressurreiten, dieses ist eine olympische Disziplin. Beim Dressurreiten präsentiert sich die gelernte und bestehende Harmonie zwischenReiter und Pferd im Ausführender verschiedenen Dressurlektionen. Ein Dressurviereck hat die Form eines Rechteckes mit einer Länge von 40 Metern undeiner Breite von 20 Metern. DasViereckist mit verschiedenen Punkten markiert. In der Abbildungist ein Teil des Vierecks dargestellt. 1 LE entspricht 1 m. Eine Dressurlektion heißt „Durch den Zirkel wechseln“.      B Nicht jedem Reiter gelingt die Ausführung der Lektion exakt, daher werden im Folgenden die Bahnen im oberenTeil des Dressurvierecks durch die Graphen der Funktionenschar f, mit der Gleichung 1.) =- ax +2a:x48 mit xeR,aeR,a>0 dargestellt. 11       Bestimmen Sie den Wert für a so, dass der Graph der Funktion f, die x-Achse in seinem Tiefpunkt berührt. 1.2      Zeigen Sie, dass sich alle Graphen in den Punkten P, (43 11. (4,8)) P,(0|f,(0)) und P, (4,3 11, (4,8)) schneiden. Ermitteln Sie zwei Parameterwerte a; und a; so, dass die beiden Graphen der Funktionen f, und f, eine Fläche mit dem Inhalt von 144 m?einschließen. 1.3      Eine weitere Lektion ist „Durch die halbe Bahn wechseln“. Der Reiter reitet entlang der Geraden g durch die Punkte K(10 | 14) und B(-10 | 0). Bestimmen Sie den Wert für a so, dass die Tangente im Wendepunkt an den Graphender Funktion f, und die Gerade g parallel zueinandersind. 1.4      Bei einem Dressurwettbewerbstarten 20 Reiter mit ihren Pferden. Die Pferde werden nachihren Farben unterschieden: Schimmel, Braune, Füchse und Rappen. 1.4.1 Jede der vier Farben kommtgleich oft vor. Es werden zufällig drei Pferde für eine medizinische Untersuchung ausgewählt und ihre Farbefestgestellt. Berechnen Sie die Wahrscheinlichkeit dafür, dass hierbei genau drei Rappen ausgewählt werden. 1.4.2 Ein Reiter behauptet, dass aufgrund ihres besonders eleganten Aussehens in der Regel mindestens 40 % Rappenan solchen Wettbewerben teilnehmen. Die Anzahl der Rappen wird als binomialverteilt angenommen. Diese Behauptung soll mit einer Irrttumswahrscheinlichkeit von 5 % getestet werden. Beim nächsten Wettbewerbsind vier der Pferde Rappen. Prüfen Sie, ob mit diesem Ergebnis die Behauptung bestätigt wird. Tabelle der Binomialverteilung (Summenfunktion) für n = 20 und p = 0,4 k           0          1           2          3        a      5          6 P(Xsk)       0,0000      0,0005     0,0036      0,0160   0,0510 0,1256     0,2500

Abitur 2013 Mathematik ohne CAS                                                    Seite 7 B2       Analytische Geometrie            (20 BE) Gegebensind die Punkte A(2|2|2), B(2|4|6), die Punkteschar C.(4|6 | a) mit aceR und die Ebene E:x+2y+3z-7=0 2.1      Zeigen Sie, dass es keinen reellen Wert für a gibt, sodass die Punkte A, B und C, auf einer Geradenliegen. 2.2      Bestimmen Sie den Wert von a, für den C, von A genau so weit entferntist wie AvonB. 2.3      BerechnenSie alle Werte von a, für die der Abstand des Punktes C, von der Geraden gıs 3 LE beträgt. 2.4      Berechnen Sie den Wert von a so, dass der Flächeninhalt des Dreiecks ABC, minimal wird. Geben Sie den minimalen Flächeninhalt an. 2.5      Die Punkte A, B und C, spanneneine Ebenenschar e, auf. GebenSie eine Gleichung von eg, in Koordinatenform an. 2.6      Gegebenist eine Ebenenschar durch die Gleichung &, :(b-10)-x+4y-2z=2b-16mitbeR. WeisenSie die Gültigkeit folgender Aussagen nach. a) Es gibt genau eine Ebene e, , die senkrecht auf E steht. b) Es gibt keine Ebene e,, die parallel zu E liegt.