CAS-Mat1-eA-Paket3.1-A-2018
Dieses Dokument ist Teil der Anfrage „Abituraufgabe Mathematik 2018 Hamburg“
Diese Anfrage wurde als Teil der Kampagne „Frag sie Abi!“ gestellt.
Freie und Hansestadt Hamburg allgemeinbildende
Behörde für Schule und Berufsbildung gymnasiale
Abitur 2018 CAS Mathematik auf erhöhtem Anforderungsniveau Oberstufen
Aufgabe II
Aufgabe II: Diabetes
Schwerpunktthema: Analysis
Gegeben ist die Funktion
1 4 4 3 13 2 8
f : x 7→ − 6
x + x − x + x + 140
10 9375 250 5
mit Definitionsbereich R.
1. a) Berechnen Sie die Koordinaten der Extrempunkte des Graphen von f und bestimmen Sie die Art
dieser Extrempunkte.
(Zur Kontrolle: Die Extremstellen sind 20, 100 und 200.) (5 BE)
b) Geben Sie die Koordinaten des Schnittpunkts des Graphen von f mit der y-Achse an.
Begründen Sie ohne weitere Rechnung, dass f genau zwei Nullstellen hat. (4 BE)
c) Für 50 < x < 130 gibt es ein Paar von x-Werten, die sich um 60 unterscheiden und für die die
zugehörigen Funktionswerte übereinstimmen.
Bestimmen Sie dieses Paar von x-Werten und geben Sie den zugehörigen Funktionswert an.
(4 BE)
d) Begründen Sie, dass sich aus den Informationen aus Teilaufgabe 1.c) schließen lässt, dass f für
50 < x < 130 mindestens eine Extremstelle hat. (3 BE)
Der Graph von f schließt mit den Koordinatenachsen und der Gerade mit der Gleichung x = 240 ein
Flächenstück ein.
e) Bestimmen Sie eine Gleichung der Gerade, die parallel zur y-Achse verläuft und dieses Flächenstück
halbiert. (4 BE)
f) Die folgende Aussage bezieht sich auf eine zweite Gerade, die das Flächenstück teilt:
240 240
Für u ≈ 217 gilt: 12 · u · f (u) + f (x) dx = 23 ·
R R
f (x) dx
u 0
Veranschaulichen Sie die Aussage unter Verwendung einer geeigneten Skizze. (4 BE)
CAS Mat1-eA-Paket3.1-A-2018 Aufgabe II, Seite 1 von 3

Freie und Hansestadt Hamburg allgemeinbildende
Behörde für Schule und Berufsbildung gymnasiale
Abitur 2018 CAS Mathematik auf erhöhtem Anforderungsniveau Oberstufen
Aufgabe II
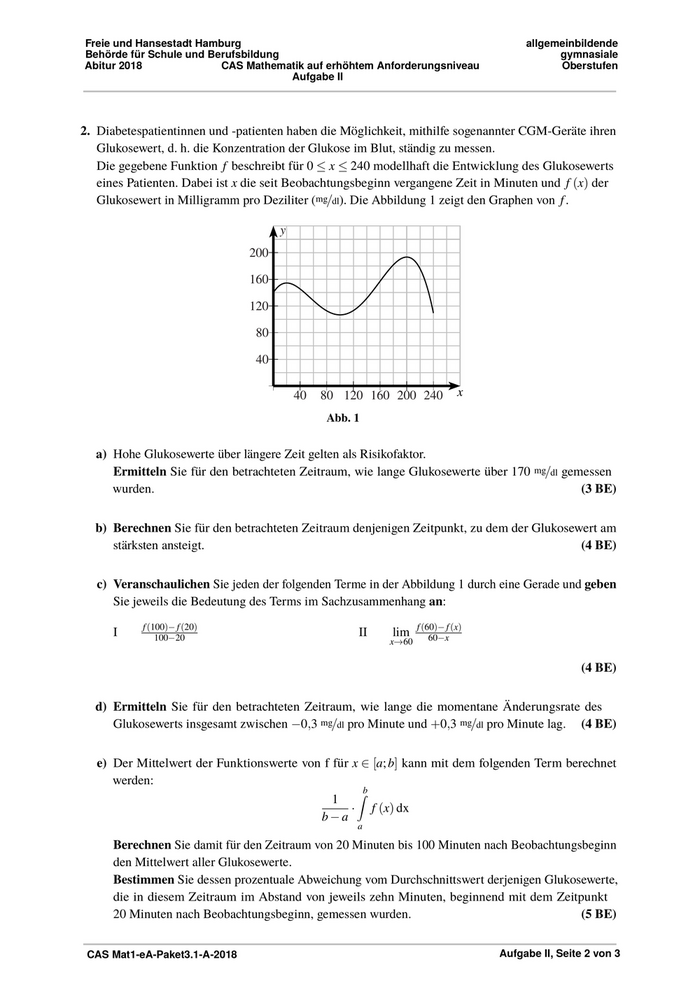
2. Diabetespatientinnen und -patienten haben die Möglichkeit, mithilfe sogenannter CGM-Geräte ihren
Glukosewert, d. h. die Konzentration der Glukose im Blut, ständig zu messen.
Die gegebene Funktion f beschreibt für 0 ≤ x ≤ 240 modellhaft die Entwicklung des Glukosewerts
eines Patienten. Dabei ist x die seit Beobachtungsbeginn vergangene Zeit in Minuten und f (x) der
Glukosewert in Milligramm pro Deziliter (mg/dl). Die Abbildung 1 zeigt den Graphen von f .
y
200
160
120
80
40
40 80 120 160 200 240 x
Abb. 1
a) Hohe Glukosewerte über längere Zeit gelten als Risikofaktor.
Ermitteln Sie für den betrachteten Zeitraum, wie lange Glukosewerte über 170 mg/dl gemessen
wurden. (3 BE)
b) Berechnen Sie für den betrachteten Zeitraum denjenigen Zeitpunkt, zu dem der Glukosewert am
stärksten ansteigt. (4 BE)
c) Veranschaulichen Sie jeden der folgenden Terme in der Abbildung 1 durch eine Gerade und geben
Sie jeweils die Bedeutung des Terms im Sachzusammenhang an:
f (100)− f (20) f (60)− f (x)
I 100−20 II lim 60−x
x→60
(4 BE)
d) Ermitteln Sie für den betrachteten Zeitraum, wie lange die momentane Änderungsrate des
Glukosewerts insgesamt zwischen −0,3 mg/dl pro Minute und +0,3 mg/dl pro Minute lag. (4 BE)
e) Der Mittelwert der Funktionswerte von f für x ∈ [a; b] kann mit dem folgenden Term berechnet
werden:
Zb
1
· f (x) dx
b−a
a
Berechnen Sie damit für den Zeitraum von 20 Minuten bis 100 Minuten nach Beobachtungsbeginn
den Mittelwert aller Glukosewerte.
Bestimmen Sie dessen prozentuale Abweichung vom Durchschnittswert derjenigen Glukosewerte,
die in diesem Zeitraum im Abstand von jeweils zehn Minuten, beginnend mit dem Zeitpunkt
20 Minuten nach Beobachtungsbeginn, gemessen wurden. (5 BE)
CAS Mat1-eA-Paket3.1-A-2018 Aufgabe II, Seite 2 von 3
Freie und Hansestadt Hamburg allgemeinbildende
Behörde für Schule und Berufsbildung gymnasiale
Abitur 2018 CAS Mathematik auf erhöhtem Anforderungsniveau Oberstufen
Aufgabe II
Zum Zeitpunkt 240 Minuten nach Beobachtungsbeginn nimmt der Patient Traubenzucker zu sich.
Die anschließende Entwicklung des Glukosewerts soll im Modell mithilfe einer Funktion g beschrie-
ben werden, die folgende Bedingung erfüllt:
Die beiden Werte, die das Modell zum Zeitpunkt 240 Minuten nach Beobachtungsbeginn
für den Glukosewert und für dessen momentane Änderungsrate liefert, sollen unabhän-
gig davon sein, ob sie mithilfe der Funktion f oder mithilfe der Funktion g ermittelt
werden.
Zur Bestimmung eines Funktionsterms von g sollen zunächst die in R definierten Funktionen
hk : x 7→ 50 − 50 · (k · x + 1)2 · e−k·x
mit k ∈ R+ betrachtet werden.
f) Bestimmen Sie den Wert von k so, dass die momentane Änderungsrate, die sich unter Verwendung
von hk für den Zeitpunkt 0 ergibt, mit der momentanen Änderungsrate übereinstimmt, die f für den
Zeitpunkt 240 Minuten nach Beobachtungsbeginn liefert. (2 BE)
g) Die für die Funktion g angegebene Bedingung lässt sich erfüllen, wenn der Graph von g durch eine
308
geeignete Verschiebung aus dem Graphen von hk für k = 3125 hervorgeht.
Beschreiben Sie diese Verschiebung und geben Sie einen Funktionsterm von g an. (4 BE)
CAS Mat1-eA-Paket3.1-A-2018 Aufgabe II, Seite 3 von 3

Freie und Hansestadt Hamburg allgemeinbildende
Behörde für Schule und Berufsbildung gymnasiale
Abitur 2018 CAS Mathematik auf erhöhtem Anforderungsniveau Oberstufen
Aufgabe III
Aufgabe III: Baumärkte
Schwerpunktthema: Lineare Algebra
In einer Stadt gab es lange Zeit nur die beiden Baumärkte A und B. Nach Eröffnung eines dritten
Baumarkts C lässt sich das Wechselverhalten der Kunden von einem Monat zum nächsten zunächst
modellhaft durch das abgebildete Übergangsdiagramm darstellen.
0,3
A
0,4 0,2
0,5 0,2
0,1
0,5 B C 0,5
0,3
Abb. 1
a) In einem Monat hat der Baumarkt A 3500 Kunden, der Baumarkt B 4840 Kunden und der Baumarkt C
1660 Kunden.
Bestimmen Sie für den vorhergehenden Monat die jeweilige Anzahl der Kunden der drei Baumärkte.
(3 BE)
Um der zunehmenden Konkurrenz durch den Baumarkt C zu begegnen, erweitert der Baumarkt A
sein Sortiment, der Baumarkt B verbessert seinen Kundenservice. Diese Maßnahmen führen zu einer
Änderung des Wechselverhaltens der Kunden.
a
Im Modell werden die Verteilungen der Kunden auf die drei Baumärkte durch Vektoren der Form b
c
dargestellt, wobei a die Anzahl der Kunden des Baumarkts A, b die Anzahl der Kunden des Baumarkts
B und c die Anzahl der Kunden des Baumarkts C bezeichnet. Damit kanndie Entwicklung der Kunden-
0,63 0,18 0,3
verteilung von einem Monat n zum nächsten nun durch die Matrix M = 0,27 0,72 0,45 und die
0,1 0,1 0,25
→
− −−→
Gleichung M · vn = vn+1 beschrieben werden.
In einem der auf die Maßnahmen folgenden Sommermonat hat der Baumarkt A 3539 Kunden, der Baumarkt
B 5281 Kunden und der Baumarkt C 1180 Kunden.
b) Weisen Sie nach, dass die beschriebenen Maßnahmen der Baumärkte A und B höchstens vier Monate
zurückliegen. (3 BE)
c) Berechnen Sie für denjenigen Monat, der dem beschriebenen Sommermonat vorherging, die
prozentualen Anteile der Kunden der drei Baumärkte an der Gesamtzahl dieser Kunden. (3 BE)
CAS Mat1-eA-Paket3.1-A-2018 Aufgabe III, Seite 1 von 2

Freie und Hansestadt Hamburg allgemeinbildende
Behörde für Schule und Berufsbildung gymnasiale
Abitur 2018 CAS Mathematik auf erhöhtem Anforderungsniveau Oberstufen
Aufgabe III
d) Ermitteln Sie auf der Grundlage des Modells, wie sich die prozentualen Anteile der Kunden der drei
Baumärkte nach der Durchführung der Maßnahmen der Baumärkte A und B langfristig entwickeln
würden, wenn das Wechselverhalten der Kunden konstant bliebe. (3 BE)
e) Geben Sie an, für welchen der drei Baumärkte der Anteil der Kunden, die nach Beginn der beschriebenen
Maßnahmen von einem Monat zum nächsten zu einem anderen Baumarkt wechseln, am kleinsten ist.
Nennen Sie den zugehörigen Anteil. (2 BE)
Der Baumarkt C muss befürchten, den für seinen wirtschaftlichen Erfolg notwendigen Anteil von 25 %
der Kunden aller drei Baumärkte nicht zu erreichen. Der Baumarkt führt deshalb Rabattaktionen durch,
mit deren Hilfe Kunden gebunden werden sollen. Ab dem Monat, in dem die Aktionen beginnen, lässt
sich das Wechselverhalten der Kunden von einem Monat zum nächsten im Modell durch eine Matrix
0,63 0,18 0,4 · (1 − p)
N = 0,27 0,72 0,6 · (1 − p)
0,1 0,1 p
mit p ∈ [0; 1] beschreiben.
f) In einem Monat nach Beginn der Rabattaktionen hat der Baumarkt A 3400 Kunden, der Baumarkt
B 5200 Kunden und der Baumarkt C 1400 Kunden. Im folgenden Monat hat der Baumarkt A 3022
Kunden.
Untersuchen Sie, ob diese Kundenzahl mit dem Modell in Einklang steht, das mithilfe der Matrix N
beschrieben wird. (3 BE)
g) Im Monat vor Beginn der Rabattaktionen hatte der Baumarkt A 3530 Kunden, der Baumarkt B 5294
Kunden und der Baumarkt C 1176 Kunden.
Ermitteln Sie ausgehend von diesen Werten, in welchem Bereich der prozentuale Anteil der Kunden
des Baumarkts C im folgenden Monat liegen kann. (3 BE)
h) Zeigen Sie, dass es für jeden Wert von p ∈ [0; 1] einen Vektor ~w gibt, dessen Komponenten nicht
negativ sind, dessen Spaltensumme 10000 ist und für den N · ~w = ~w gilt.
Bestimmen Sie für einen geeignet gewählten Wert von p einen Vektor ~w, dessen Komponenten
ganzzahlig sind.
Interpretieren Sie die Bedeutung dieses Vektors im Sachzusammenhang.
(5 BE)
CAS Mat1-eA-Paket3.1-A-2018 Aufgabe III, Seite 2 von 2

Freie und Hansestadt Hamburg allgemeinbildende
Behörde für Schule und Berufsbildung gymnasiale
Abitur 2018 CAS Mathematik auf erhöhtem Anforderungsniveau Oberstufen
Aufgabe IV
Aufgabe IV: Kunststoffteile
Schwerpunktthema: Stochastik
1. Für ein Spiel wird ein Glücksrad verwendet, das drei farbige Sektoren hat. Der Tabelle können die
Farben der Sektoren und die Größen der zugehörigen Mittelpunktswinkel entnommen werden.
Farbe Blau Rot Grün
Mittelpunktswinkel 180◦ 120◦ 60◦
Für einen Einsatz von 5 Euro darf ein Spieler das Glücksrad dreimal drehen. Erzielt der Spieler
dreimal die gleiche Farbe, werden ihm 10 Euro ausgezahlt. Erzielt er drei verschiedene Farben, wird
ein anderer Betrag ausgezahlt. In allen anderen Fällen erfolgt keine Auszahlung.
Die Wahrscheinlichkeit dafür, dass dreimal die gleiche Farbe erzielt wird, ist 16 .
a) Zeigen Sie, dass die Wahrscheinlichkeit dafür, dass drei verschiedene Farben erzielt werden,
ebenfalls 16 beträgt. (2 BE)
b) Bei dem Spiel ist zu erwarten, dass sich die Einsätze der Spieler und die Auszahlungen auf lange
Sicht ausgleichen.
Berechnen Sie den Betrag, der ausgezahlt wird, wenn drei verschiedene Farben erscheinen. (3 BE)
c) Die Größen der Sektoren werden geändert. Dabei wird der blaue Sektor vergrößert. Die Abbildung 1
zeigt einen Teil eines Baumdiagramms, das für das geänderte Glücksrad die drei Drehungen
beschreibt. Ergänzend ist für einen Pfad die zugehörige Wahrscheinlichkeit angegeben.
B 0,036
R R R
2p
p
G G
Abb. 1
Bestimmen Sie die Größe des zum blauen Sektor gehörenden Mittelpunktswinkels. (5 BE)
CAS Mat1-eA-Paket3.1-A-2018 Aufgabe IV, Seite 1 von 2

Freie und Hansestadt Hamburg allgemeinbildende
Behörde für Schule und Berufsbildung gymnasiale
Abitur 2018 CAS Mathematik auf erhöhtem Anforderungsniveau Oberstufen
Aufgabe IV
2. Ein Unternehmen stellt Kunststoffteile her. Erfahrungsgemäß sind 4 % der hergestellten Teile fehlerhaft.
Die Anzahl fehlerhafter Teile unter zufällig ausgewählten kann als binomialverteilt angenommen werden.
a) 800 Kunststoffteile werden zufällig ausgewählt.
Berechnen Sie für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:
A: „Genau 30 der Teile sind fehlerhaft.“
B: „Mindestens 5% der Teile sind fehlerhaft.“
(3 BE)
b) Ermitteln Sie, wie viele Kunststoffteile mindestens zufällig ausgewählt werden müssen, damit
davon mit einer Wahrscheinlichkeit von mindestens 95 % mindestens 100 Teile keinen Fehler haben.
(4 BE)
Die Kunststoffteile werden aus Kunststoffgranulat hergestellt. Nach einem Wechsel des Granulats
vermutet der Produktionsleiter, dass sich der Anteil der fehlerhaften Teile reduziert hat.
Daher soll ein Hypothesentest mit einer Stichprobe von 500 Teilen auf einem Signifikanzniveau von 5 %
durchgeführt werden. Dabei wird die Nullhypothese wie folgt gewählt: „Der Anteil der fehlerhaften Tei-
le beträgt mindestens 4 %.“
c) Bestimmen Sie die zugehörige Entscheidungsregel. (5 BE)
d) Das neue Granulat ist teurer als das vorherige.
Geben Sie an, welche Überlegung zur Wahl der Nullhypothese geführt haben könnte, und begründen
Sie Ihre Angabe. (3 BE)
CAS Mat1-eA-Paket3.1-A-2018 Aufgabe IV, Seite 2 von 2







