M GK HT 1 Seite 1 von 2 Name: _______________________ Abiturprüfung 2014 Mathematik, Grundkurs Aufgabenstellung: Die Funktion f ist gegeben durch f  x    2  x   e , x  IR . x Die Graphen der Funktion f und ihrer Ableitungsfunktion f  sind in der Abbildung dargestellt. y f x Abbildung a) (1) Berechnen Sie die Koordinaten der Schnittpunkte des Graphen von f mit den Koordinatenachsen. (2) Bestimmen Sie rechnerisch die Koordinaten der Extrem- und Wendepunkte des Graphen von f. [Zur Kontrolle: f   x   1  x   e ] x (3) Untersuchen Sie, ob sich die Graphen der Funktionen f und f  schneiden. (5 + 16 + 4 Punkte) Nur für den Dienstgebrauch!

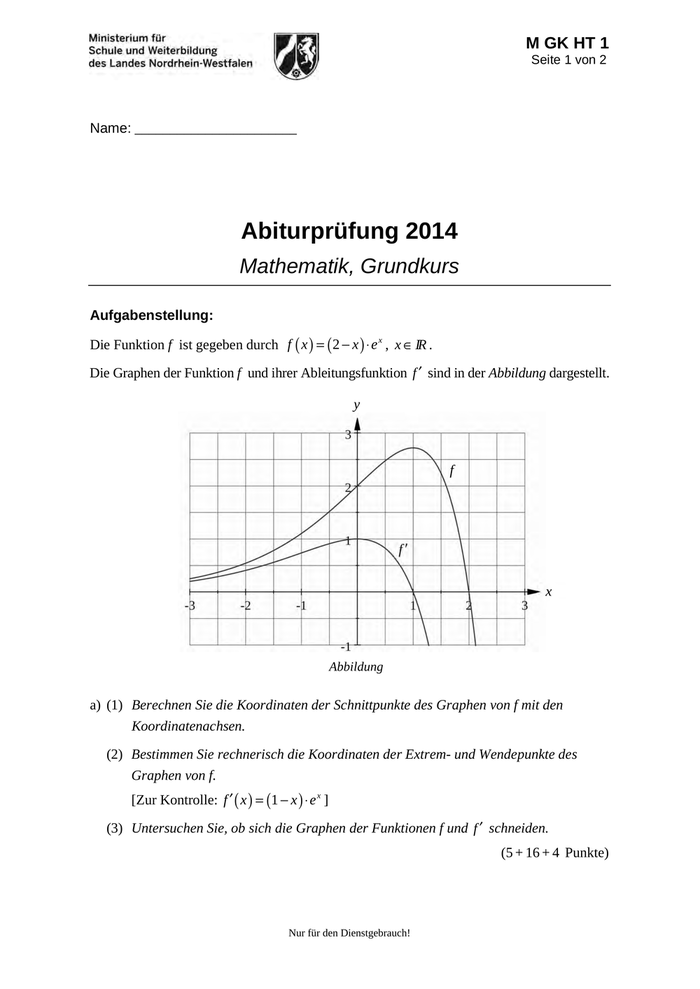
M GK HT 1 Seite 2 von 2 Name: _______________________ b) (1) Zeigen Sie, dass die Funktion F mit der Gleichung F  x    3  x   e eine Stamm- funktion von f ist. x (2) Ermitteln Sie für 0  z  2 den Inhalt A  z  der zwischen dem Graphen von f und der x-Achse im Intervall [0; z ] eingeschlossenen Fläche in Abhängigkeit von z. [Zur Kontrolle: A  z    3  z   e  3 ] z (4 + 6 Punkte) c) Auf einem Erdölfeld wird Öl gefördert. Durch die Funktion f wird nun für 0  x  2 die 1 Förderrate von Beginn des Jahres 2013 bis Ende des Jahres 2014 modelliert. Dabei wird x als Maßzahl der Zeit zur Einheit 1 Jahr und f  x  als Maßzahl der Förderrate zur Einheit 1 Million Tonnen pro Jahr aufgefasst. (1) Beschreiben Sie den Verlauf des Graphen von f im Intervall [0; 2] im Sachzusammen- hang. (2) Bestimmen Sie die für den gesamten Zeitraum von Beginn des Jahres 2013 bis Ende des Jahres 2014 zu erwartende Fördermenge. (3) Am Ende des ersten Quartals 2014 erkennt der Betreiber, dass die Förderrate von diesem Zeitpunkt an – im Gegensatz zur Modellierung durch die Funktion f – bis zum Ende der Ölförderung linear abnehmen wird. Zur Darstellung der Förderrate für die verbleibende Dauer der Ölförderung wird daher eine lineare Funktion g 5 gesucht, deren Graph zum Zeitpunkt x  dieselbe Steigung hat wie der Graph 4 der Funktion f. Ermitteln Sie eine Gleichung dieser Funktion g. Berechnen Sie den Zeitpunkt, zu dem die Ölförderung enden wird. 5 4 1 [Zur Kontrolle: g  x   e  17  4 x  ] 16 Zugelassene Hilfsmittel:  Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit)  Mathematische Formelsammlung  Wörterbuch zur deutschen Rechtschreibung 1 Unter Förderrate ist stets die momentane Förderrate zu verstehen. Nur für den Dienstgebrauch! (3 + 4 + 8 Punkte)

Ministerium für Schule und Weiterbildung NRW M GK HT 1 Seite 1 von 6 Unterlagen für die Lehrkraft Abiturprüfung 2014 Mathematik, Grundkurs 1. Aufgabenart Analysis 2. 1 Aufgabenstellung siehe Prüfungsaufgabe 3. Materialgrundlage  entfällt 4. Bezüge zu den Vorgaben 2014 1. Inhaltliche Schwerpunkte  Untersuchung von ganzrationalen Funktionen einschließlich Funktionenscharen und Exponentialfunktionen in Sachzusammenhängen, notwendiger Ableitungsregeln (Produkt- und Kettenregel)  Untersuchungen von Wirkungen (Änderungsrate)  Flächenberechnung durch Integration 2. Medien/Materialien  entfällt 5. Zugelassene Hilfsmittel  Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit)  Mathematische Formelsammlung  Wörterbuch zur deutschen Rechtschreibung 1 Die Aufgabenstellung deckt inhaltlich alle drei Anforderungsbereiche ab. Nur für den Dienstgebrauch!

M GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 2 von 6 6. Modelllösungen Die jeweilige Modelllösung stellt eine mögliche Lösung bzw. Lösungsskizze dar. Der gewählte Lösungsansatz und -weg der Schülerinnen und Schüler muss nicht identisch mit dem der Modelllösung sein. Sachlich richtige Alternativen werden mit entsprechender Punktzahl bewertet (Bewertungsbogen: Zeile „Sachlich richtige Lösungsalternative zur Modelllösung“). Teilaufgabe a) (1) f  0    2  0   e  2 . 0 f  x   0  2  x   e  0  x  2 . x Schnittpunkt mit der y-Achse:  0 | 2  , Schnittpunkt mit der x-Achse:  2 | 0  .  x x x (2) f   x     2  x   e   1  e   2  x   e  1  x   e . x f   xE   0  1  xE   e  0  xE  1 . Da die Funktion f  an der Stelle x E  1 das xE Vorzeichen von + nach – wechselt, ist f  xE   e lokales Maximum von f. H 1 | e  ist Hochpunkt des Graphen von f.  x x x f   x    1  x   e   1  e  1  x   e   x  e . x f   xW   0   xW  e xW  0  xW  0 . Da die Funktion f  an der Stelle xW  0 das Vorzeichen wechselt, ist xW Wendestelle von f. W  0 | 2 ist Wendepunkt des Graphen von f. (3) Wegen f  xS   f   xS    2  xS   e  1  xS   e  e  0 hat die Gleichung xS xS xS f  xS   f   xS  keine Lösung. Daher haben die Graphen von f und f  keinen Schnittpunkt. Nur für den Dienstgebrauch!

M GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 3 von 6 Teilaufgabe b)  x x x (1) Wegen F   x     3  x   e   1  e   3  x   e   2  x   e  f  x  ist F eine x Stammfunktion von f. (2) Für 0  x  2 gilt f  x    2  x   e  0 . Daher ist x z A  z    f  x  dx 0  F  z  F 0  3  z   e  3  e z 0  3  z   e  3 z der gesuchte Flächeninhalt. Teilaufgabe c) (1) Die Förderrate steigt von 2 Millionen Tonnen pro Jahr zu Beginn des Jahres 2013 2 [streng monoton] auf den Höchstwert von ca. 2,72 Millionen Tonnen pro Jahr am Ende des Jahres an. Danach nimmt sie [streng monoton] bis zum Ende des Jahres 2014 auf Null ab. (2) Die gesamte Fördermenge der Jahre 2013 und 2014 entspricht dem Inhalt der vom Graphen von f und den Koordinatenachsen im 1. Quadranten eingeschlossenen Fläche. Mit dem Kontrollergebnis von b) (2) ergibt sich: A  2    3  2   e  3  e  3  4,39 . 2 Die gesamte Fördermenge beträgt ca. 4,39 Millionen Tonnen. 2 Unter „Förderrate“ ist stets die „momentane Förderrate“ zu verstehen. Nur für den Dienstgebrauch! 2

Ministerium für Schule und Weiterbildung NRW M GK HT 1 Seite 4 von 6 5 (3) Dem Ende des 1. Quartals 2014 entspricht der Zeitpunkt x  . 4 5 Für x  [ x  x0 (siehe unten)] kann die Förderrate durch die lineare Funktion g 4 5 5 5 dargestellt werden, für die g    f   und g  x   f    gilt. 4 4 4 5 5 5  g  x  f    x    f   4 4 4  5 4 5 5  5    1    e  x     2    e 4 4  4   5 4 1 5 3    e  x    e 4 4 4  5 4 5 4 5 4 1 12  e  5  4 x    e 16 16 5 1 4  e  17  4 x  . 16 5 4 Der Zeitpunkt x0 , zu dem die Ölförderung endet, ist die Nullstelle der Funktion g. 17 g  x0   0  x0  : Mit Ablauf des 1. Quartals 2017 wird die Ölförderung enden. 4 Nur für den Dienstgebrauch!

M GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 5 von 6 7. Teilleistungen – Kriterien / Bewertungsbogen zur Prüfungsarbeit Name des Prüflings:__________________________________ Kursbezeichnung:_________ Schule: _____________________________________________ Teilaufgabe a) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl 1 (1) berechnet die Koordinaten der Schnittpunkte des Graphen von f mit den Koordinatenachsen. 5 2 (2) berechnet f   x  . 3 3 (2) bestimmt rechnerisch die Koodinaten des Hochpunktes. 5 4 (2) berechnet f   x  . 3 5 (2) bestimmt rechnerisch die Koodinaten des Wendes- punktes. 5 6 (3) untersucht, ob sich die Graphen von f und f  schneiden. 4 EK 3 ZK DK Sachlich richtige Lösungsalternative zur Modelllösung: (25) …………………………………………………………………… …………………………………………………………………… Summe Teilaufgabe a) 25 Teilaufgabe b) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl 1 (1) zeigt, dass die Funktion F eine Stammfunktion von f ist. 4 2 (2) ermittelt A  z  . 6 Sachlich richtige Lösungsalternative zur Modelllösung: (10) …………………………………………………………………… …………………………………………………………………… Summe Teilaufgabe b) 3 10 EK = Erstkorrektur; ZK = Zweitkorrektur; DK = Drittkorrektur Nur für den Dienstgebrauch! EK ZK DK

M GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 6 von 6 Teilaufgabe c) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl 1 (1) beschreibt den Verlauf des Graphen von f im Intervall [0; 2] im Sachzusammenhang. 3 2 (2) bestimmt die für den gesamten Zeitraum von Beginn des Jahres 2013 bis Ende des Jahres 2014 zu erwartende Fördermenge. 4 3 (3) ermittelt eine Gleichung der Funktion g. 5 4 (3) berechnet den Zeitpunkt, zu dem die Ölförderung enden wird. 3 EK ZK Sachlich richtige Lösungsalternative zur Modelllösung: (15) …………………………………………………………………… …………………………………………………………………… Summe Teilaufgabe c) 15 Summe insgesamt 50 Die Festlegung der Gesamtnote der Prüfungsleistung erfolgt auf dem Bewertungsbogen einer Aufgabe aus der Aufgabengruppe 2. Nur für den Dienstgebrauch! DK

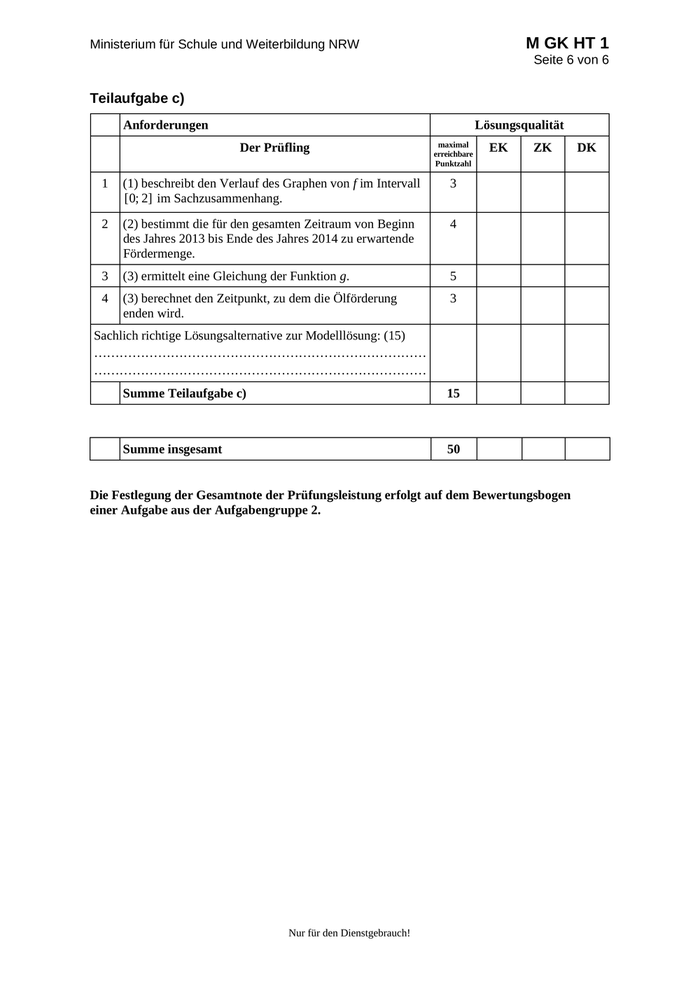
M GK HT 2 Seite 1 von 3 Name: _______________________ Abiturprüfung 2014 Mathematik, Grundkurs Aufgabenstellung: 1 In ein Staubecken oberhalb eines Bergdorfes fließt ein Bach. Die momentane Zuflussrate aus dem Bach kann an einem Tag mit starken Regenfällen durch die Funktion f mit der Gleichung 1 3 2 f  t   t  12t  144t  250 , t  IR , 4 für einen bestimmten Beobachtungszeitraum modelliert werden. Dabei fasst man t als 3 Maßzahl zur Einheit 1 h und f  t  als Maßzahl zur Einheit 1 m /h auf. Der Beobachtungs- zeitraum beginnt zum Zeitpunkt t  0 und endet zum Zeitpunkt t  24 . 3 [m /h] t [h] Abbildung 1 Im Folgenden wird zur besseren Lesbarkeit nur der Begriff Zuflussrate verwendet; darunter ist stets die momentane Zuflussrate zu verstehen. Nur für den Dienstgebrauch!

M GK HT 2 Seite 2 von 3 Name: _______________________ a) (1) Berechnen Sie die Zuflussrate zu Beginn und am Ende des Beobachtungszeitraums. (2) Bestimmen Sie den Zeitpunkt tm  [0; 24] , zu dem die Zuflussrate ihr Maximum annimmt, und berechnen Sie dieses Maximum. (3 + 9 Punkte) b) (1) Bestimmen Sie die Wendestelle des Graphen der Funktion f. (2) Bestimmen Sie den Zeitpunkt des Beobachtungszeitraums, zu dem sich die Zufluss- rate am stärksten ändert. (3) Geben Sie nun die Bedeutung der Wendestelle aus (1) im Sachzusammenhang an. (4) Geben Sie einen Zeitraum an, in dem die Funktion f die Zuflussrate nicht sinnvoll beschreiben könnte, und begründen Sie dies. (6 + 6 + 3 + 4 Punkte) 3 c) Zum Zeitpunkt t  0 kann das Staubecken noch 4 500 m Wasser aufnehmen. (1) Entscheiden Sie, ob das Staubecken das gesamte Wasser aus dem Bach während der 24 Stunden des Beobachtungszeitraums aufnehmen könnte. a (2) Die Gleichung  f  t  dt  4 500 hat die (positive) Lösung a  7,6 . 0 Geben Sie die Bedeutung dieser Lösung im Sachzusammenhang an. Um ein Überlaufen des Staubeckens zu verhindern, wird zum Zeitpunkt t  6 ein vorher verschlossener Notablauf geöffnet. Durch diesen fließt Wasser mit einer konstanten Ab- 3 flussrate von 600 m /h aus dem Staubecken ab. Der Notablauf bleibt bis zum Ende des Beobachtungszeitraums geöffnet. Ohne Nachweis darf verwendet werden, dass die Zu- 3 flussrate für 6  t  14 größer und für 14  t  24 kleiner als 600 m /h ist (vgl. Abbil- dung auf Seite 1). 6 14 0 6 (3) Interpretieren Sie den Ausdruck  f  t  dt    f  t   600  dt im Sachzusammenhang. Geben Sie insbesondere die Bedeutung des Zeitpunkts t  14 an. (4) Entscheiden Sie nun, ob das Staubecken innerhalb des Beobachtungszeitraums überläuft. (5 + 3 + 6 + 5 Punkte) Nur für den Dienstgebrauch!