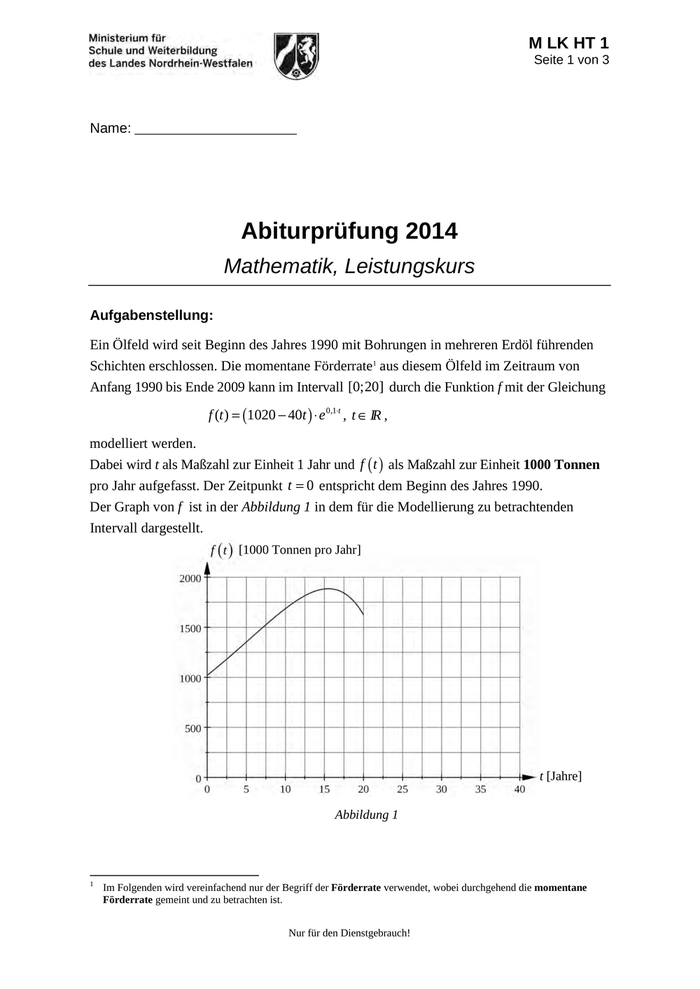
M LK HT 1 Seite 1 von 3 Name: _______________________ Abiturprüfung 2014 Mathematik, Leistungskurs Aufgabenstellung: Ein Ölfeld wird seit Beginn des Jahres 1990 mit Bohrungen in mehreren Erdöl führenden 1 Schichten erschlossen. Die momentane Förderrate aus diesem Ölfeld im Zeitraum von Anfang 1990 bis Ende 2009 kann im Intervall [0;20] durch die Funktion f mit der Gleichung f (t )  1020  40t   e 0,1t , t  IR , modelliert werden. Dabei wird t als Maßzahl zur Einheit 1 Jahr und f  t  als Maßzahl zur Einheit 1000 Tonnen pro Jahr aufgefasst. Der Zeitpunkt t  0 entspricht dem Beginn des Jahres 1990. Der Graph von f ist in der Abbildung 1 in dem für die Modellierung zu betrachtenden Intervall dargestellt. [1000 Tonnen pro Jahr] t [Jahre] Abbildung 1 1 Im Folgenden wird vereinfachend nur der Begriff der Förderrate verwendet, wobei durchgehend die momentane Förderrate gemeint und zu betrachten ist. Nur für den Dienstgebrauch!

M LK HT 1 Seite 2 von 3 Name: _______________________ a) Bestimmen Sie rechnerisch den Zeitpunkt im betrachteten Zeitraum von Anfang 1990 bis Ende 2009, zu dem die Förderrate maximal ist, und berechnen Sie den Maximalwert. [Zur Kontrolle: f   t    62  4t   e 0,1t ] (11 Punkte) b) Die Menge des Erdöls, das seit dem Beginn der Ölförderung Anfang 1990 bis zu einem beliebigen Zeitpunkt t des betrachteten Zeitraums aus dem Ölfeld gefördert wurde, wird durch eine Funktion M : t  M (t ) , 0  t  20 , beschrieben. (1) Bestimmen Sie eine Gleichung dieser Funktion M. [Zur Kontrolle: Eine Stammfunktion der Funktion f ist die Funktion F mit der 0,1  t Gleichung F (t )  14 200  400t   e .] (2) Berechnen Sie die gesamte Fördermenge aus dem Ölfeld von Anfang 1990 bis Ende 2009. (3) Ermitteln Sie die Einnahmen aus dem Verkauf des im Jahr 2007 geförderten Erdöls, wenn man von einem Verkaufspreis von 56 Euro pro Barrel im Jahr 2007 ausgeht. 1 Barrel Erdöl (ca. 159 Liter) wiegt ca. 137 kg. (8 + 3 + 6 Punkte) Seit Anfang des Jahres 2010 schwächt sich der Rückgang der Förderrate ab. Diese soll im Intervall ] 20; 40] daher durch die Funktion g mit der Gleichung g(t )  180  e 4  0,1  t  40  e , t  IR , 2 modelliert werden. Dabei wird wieder t als Maßzahl zur Einheit 1 Jahr und g  t  als Maß- zahl zur Einheit 1000 Tonnen pro Jahr aufgefasst. Der Zeitpunkt t  20 entspricht dem Be- ginn des Jahres 2010. Die Abbildung 2 auf Seite 3 stellt die Graphen der Funktionen f und g in den jeweils für die Modellierung zu betrachtenden Intervallen dar. c) (1) Begründen Sie anhand des Funktionsterms von g, warum die Funktion g die För- derrate nicht über einen längeren Zeitraum sinnvoll beschreiben könnte. (2) Der Betreiber kalkuliert, dass die Ölförderung für ihn nur wirtschaftlich ist, wenn innerhalb eines Kalenderjahres mindestens 600 000 Tonnen Öl gefördert werden. Bestimmen Sie das letzte Kalenderjahr, für das die Ölförderung wirtschaftlich sein wird. [Zur Kontrolle: Die Fördermenge im Intervall [T ; T  1] , 20  T  39 , lässt sich durch J  T   40  e  1800  e 2 4  0,1 T  1  e 0,1  ermitteln.] Nur für den Dienstgebrauch! (4 + 10 Punkte)

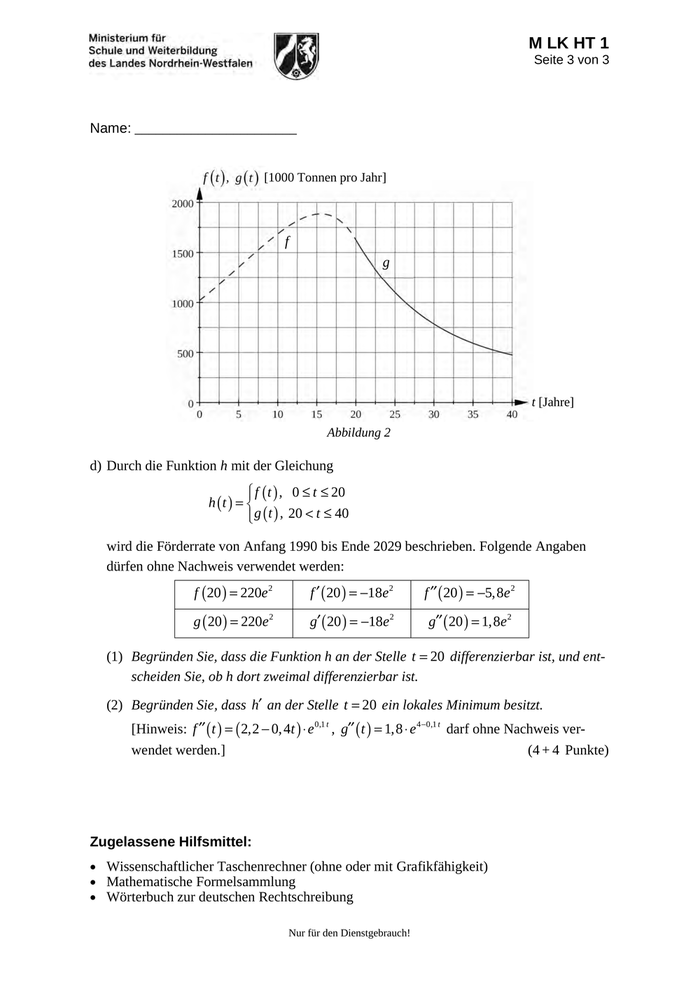
M LK HT 1 Seite 3 von 3 Name: _______________________ , [1000 Tonnen pro Jahr] f g t [Jahre] Abbildung 2 d) Durch die Funktion h mit der Gleichung  f  t  , 0  t  20 h t     g  t  , 20  t  40 wird die Förderrate von Anfang 1990 bis Ende 2029 beschrieben. Folgende Angaben dürfen ohne Nachweis verwendet werden: f  20   220e 2 g  20   220e 2 f   20   18e 2 g  20   18e 2 f   20   5,8e g  20   1,8e 2 2 (1) Begründen Sie, dass die Funktion h an der Stelle t  20 differenzierbar ist, und ent- scheiden Sie, ob h dort zweimal differenzierbar ist. (2) Begründen Sie, dass h an der Stelle t  20 ein lokales Minimum besitzt. [Hinweis: f   t    2,2  0, 4t   e wendet werden.] 0,1 t , g  t   1,8  e 4  0,1 t darf ohne Nachweis ver- (4 + 4 Punkte) Zugelassene Hilfsmittel:  Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit)  Mathematische Formelsammlung  Wörterbuch zur deutschen Rechtschreibung Nur für den Dienstgebrauch!

Ministerium für Schule und Weiterbildung NRW M LK HT 1 Seite 1 von 6 Unterlagen für die Lehrkraft Abiturprüfung 2014 Mathematik, Leistungskurs 1. Aufgabenart Analysis 2. 1 Aufgabenstellung siehe Prüfungsaufgabe 3. Materialgrundlage  entfällt 4. Bezüge zu den Vorgaben 2014 1. Inhaltliche Schwerpunkte  Untersuchung von ganzrationalen Funktionen und Exponentialfunktionen einschließ- lich Funktionenscharen sowie Logarithmusfunktionen in Sachzusammenhängen, notwendige Ableitungsregeln (Produktregel, Quotientenregel, Kettenregel)  Untersuchung von Wirkungen (Integral der Änderungsrate)  Integrationsregeln (partielle Integration, Substitution)  Flächenberechnung durch Integration 2. Medien/Materialien  entfällt 5. Zugelassene Hilfsmittel  Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit)  Mathematische Formelsammlung  Wörterbuch zur deutschen Rechtschreibung 1 Die Aufgabenstellung deckt inhaltlich alle drei Anforderungsbereiche ab. Nur für den Dienstgebrauch!

M LK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 2 von 6 6. Modelllösungen Die jeweilige Modelllösung stellt eine mögliche Lösung bzw. Lösungsskizze dar. Der gewählte Lösungsansatz und -weg der Schülerinnen und Schüler muss nicht identisch mit dem der Modelllösung sein. Sachlich richtige Alternativen werden mit entsprechender Punktzahl bewertet (Bewertungsbogen: Zeile „Sachlich richtige Lösungsalternative zur Modelllösung“). Teilaufgabe a) Gesucht ist das globale Maximum der Funktion f auf dem abgeschlossenen Intervall [0;20]. Dieses kann dort nur an einer Nullstelle von f  oder einer Randstelle angenommen werden. f   t    1020  40t   e 0,1t   0,1t 0,1t    1020  40t   e  1020  40t    e   40  e 0,1t  0,1  1020  40t   e   62  4t   e 0,1t 0,1t f   t m   0   62  4t m   e 0,1tm  0  62  4t m  0  t m  15,5 . Aus dem Vergleich der Werte f  0   1020 , f  t m   400  e 1,55  1884,6 und f  20   220  e  1625,6 folgt, f  t m  ist das gesuchte globale Maximum. 2 Die Förderrate ist Mitte des Jahres 2005 mit ca. 1,88 Millionen Tonnen pro Jahr maximal. Teilaufgabe b) (1) Stammfunktion von f: F  t    (1020  40t )  e 0,1t dt  (1020  40t )  10  e 0,1t  (1020  40t )  10  e 0,1t  14 200  400t   e 0,1t   40 10  e  4000  e 0,1t 0,1t dt C  C , C  IR . Für C  0 erhält man das Kontrollergebnis. Die gesuchte Funktion ist diejenige Stammfunktion M von f, für die M  0   0 gilt. Es ergibt sich C  14 200 und somit M (t )  14 200  400t   e Nur für den Dienstgebrauch! 0,1t  14 200 .

M LK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 3 von 6 (2) M (20)  14 200  400  20   e 0,120  14 200  6 200  e  14 200  31612 . 2 Von Anfang 1990 bis Ende 2009 wurden rund 31,6 Millionen Tonnen Erdöl aus dem Ölfeld gefördert. (3) M  18   M 17    14 200  400  18   e  7 000  e  7 400  e  1840,32. 1,8 0,1  18  14 200  400  17   e 0,1  17 1,7 Im Jahr 2007 wurden ca. 1,84032 Millionen Tonnen Erdöl gefördert. Daraus ergeben sich für das Jahr 2007 Einnahmen von rund kg  Euro  6   1840,32 10 kg : 137 56   Barrel  Barrel  Euro 6  13, 433  10 Barrel   56 Barrel  752 Millionen Euro. Teilaufgabe c) (1) Für große t streben die Funktionswerte von g gegen lim g(t )  40  e  295,6  0 , die 2 t  Förderrate nähert sich somit einem konstanten positiven Wert. Das Ölfeld hätte – im Widerspruch zur Realität – unerschöpfliche Ölreserven. (2) Die Fördermenge eines Jahres lässt sich durch J  T   T 1  g  t  dt , 20  T  39 , ermitteln. T Die Funktion G mit der Gleichung G  t   40  e  t  1800  e 2 4  0,1  t ist eine Stamm- funktion der Funktion g. Es gilt: J T   G T  1  G T    40  e   T  1   1800  e 2 4  0,1 T 1  40  e  T  40  e  1800  e 2  40  e  1800  e 2 2 4  0,1 T 4  0,1 T  1  e 0,1     40  e  T  1800  e 2 e 0,1 4  0,1 T  40  e  T  1800  e 2 Nur für den Dienstgebrauch!  4  0,1 T

M LK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 4 von 6 Ermittlung des Zeitpunktes T0 , für den die im Zeitraum [T0 ; T0  1] geförderte Menge Erdöl 600 000 Tonnen beträgt: J  T0   600 e 4  0,1 T0 600  40  e  0,1 1800  1  e  2  600  40  e2    4  0,1  T0  ln  0,1  1800  1  e       600  40  e 2     4  T0  10   ln   0,1   1800  1  e       T0  34,249 Die Funktion g ist wegen g  t   18  e 4  0,1  t  0 streng monoton fallend. [Wegen J   T   g  T  1   g  T   0 ist auch die Funktion T  J  T  , 20  T  39 , streng monoton fallend.] Daher wird die Förderung letztmals im Kalenderjahr 2024 wirtschaftlich sein. Teilaufgabe d) (1) Die Funktionen f  und g sind auf IR definiert. Wegen f  20   g  20  und f   20   g  20  ist die Funktion h an der Stelle t  20 differenzierbar. Wäre h an der Stelle t  20 diffenzierbar, so müsste f   20   g  20  gelten. Folglich ist die Funktion h an der Stelle t  20 nicht zweimal differenzierbar. [Konventionen aus dem Unterricht über zusammengesetzte Funktionen können berück- sichtigt werden.] (2) Für 0  t  20 gilt h  t   f   t    2,2  0, 4t   e h  t   g  t   1, 8  e 4  0,1 t 0,1 t , für 20  t  40 gilt . Für 5,5  t  20 ist h  t  negativ, h somit streng monoton fallend, für 20  t  40 ist h  t  positiv, h somit streng monoton steigend. Folglich besitzt h an der Stelle t  20 ein lokales Minimum. Nur für den Dienstgebrauch!

M LK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 5 von 6 7. Teilleistungen – Kriterien / Bewertungsbogen zur Prüfungsarbeit Name des Prüflings:__________________________________ Kursbezeichnung:_________ Schule: _____________________________________________ Teilaufgabe a) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl 1 berechnet die erste Ableitung von f. 3 2 bestimmt rechnerisch den Zeitpunkt im betrachteten Zeit- raum, zu dem die Förderrate maximal ist, und berechnet diesen Maximalwert. 8 EK 2 ZK DK Sachlich richtige Lösungsalternative zur Modelllösung: (11) …………………………………………………………………… …………………………………………………………………… Summe Teilaufgabe a) 11 Teilaufgabe b) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl 1 (1) bestimmt eine Gleichung einer Stammfunktion von f. 5 2 (1) bestimmt eine Gleichung der Funktion M. 3 3 (2) berechnet die gesamte Fördermenge aus dem Ölfeld von Anfang 1990 bis Ende 2009. 3 4 (3) ermittelt die im Jahr 2007 geförderte Erdölmenge. 3 5 (3) berechnet die Einnahmen aus dem Verkauf des im Jahr 2007 geförderten Erdöls. 3 Sachlich richtige Lösungsalternative zur Modelllösung: (17) …………………………………………………………………… …………………………………………………………………… Summe Teilaufgabe b) 2 17 EK = Erstkorrektur; ZK = Zweitkorrektur; DK = Drittkorrektur Nur für den Dienstgebrauch! EK ZK DK

M LK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 6 von 6 Teilaufgabe c) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl 1 (1) begründet anhand des Funktionsterms von g, warum die Funktion g die Förderrate nicht über einen längeren Zeitraum sinnvoll beschreiben könnte. 4 2 (2) bestimmt das letzte Kalenderjahr, in dem die Förderung wirtschaftlich sein wird. 10 EK ZK DK Sachlich richtige Lösungsalternative zur Modelllösung: (14) …………………………………………………………………… …………………………………………………………………… Summe Teilaufgabe c) 14 Teilaufgabe d) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl 1 (1) begründet, dass die Funktion h an der Stelle t  20 differenzierbar ist, und entscheidet, ob h an der Stelle t  20 zweimal differenzierbar ist. 4 2 (2) begründet, dass h an der Stelle t = 20 ein lokales Minimum besitzt. 4 EK ZK Sachlich richtige Lösungsalternative zur Modelllösung: (8) …………………………………………………………………… …………………………………………………………………… Summe Teilaufgabe d) 8 Summe insgesamt 50 Die Festlegung der Gesamtnote der Prüfungsleistung erfolgt auf dem Bewertungsbogen einer Aufgabe aus der Aufgabengruppe 2. Nur für den Dienstgebrauch! DK

M LK HT 2 Seite 1 von 3 Name: _______________________ Abiturprüfung 2014 Mathematik, Leistungskurs Aufgabenstellung: In ein Staubecken oberhalb eines Bergdorfes fließen zwei Bäche. Nach Regenfällen unter- 1 schiedlicher Dauer und Stärke können die momentanen Zuflussraten aus den beiden Bächen durch Funktionen fa für den Bach 1 und ga für den Bach 2 und die Gesamtzuflussrate aus den beiden Bächen durch eine Funktion ha für einen bestimmten Beobachtungszeitraum modelliert werden. Gegeben sind für a  0 zunächst die Funktionsgleichungen 1 3 2 2 fa  t   t  3a  t  9a  t  340 , t  IR , und 4 1 3 2 2 ha  t   t  7a  t  24a  t  740 , t  IR . 2 Dabei fasst man t als Maßzahl zur Einheit 1 h und fa  t  , ga  t  sowie ha  t  als Maßzahlen 3 zur Einheit 1 m /h auf. Der Beobachtungszeitraum beginnt zum Zeitpunkt t  0 und endet zum Zeitpunkt t  6a . Die Graphen von f4 , g4 und h4 sind in der Abbildung dargestellt. 3 [m /h] t [h] Abbildung 1 Im Folgenden wird zur besseren Lesbarkeit nur der Begriff Zuflussrate verwendet; darunter ist stets die momentane Zuflussrate zu verstehen. Nur für den Dienstgebrauch!