Aufsaben 1 und 2 eA Analvtische Geometrie OHNE CAS

Punkteverteilung Aufgabe 1:

atom I I I Irre
zweikoretor | | | [| I I

 

a) Gegeben ist die Funktionenschar f, mit der Funktionsgleichung:
f,. &)=a'x*-2'x?+4 mitaxeRunda #0.

Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind und begründen Sie Ihre
Entscheidung.

Entscheidung und Begründung

Alle Funktionsgraphen
der Funktionenschar
sind achsensym-
metrisch.

Für a > 0 kann die
Funktion drei Extrema
besitzen.

 

Alle Funktionsgraphen
der Funktionenschar
besitzen zwei
Wendepunkte.

b) Gegeben sind Parabeln, deren Verläufe durch fı(x) = —x2 — Zx mit,xe Rundt>0
beschrieben werden.

Weisen Sie nach, dass die Flächen, die die Parabeln mit der Abszisse einschließen, für
allet > 0 gleich groß sind.

Zentrale Abschlussprüfung Mathematik BG 04. April 2014
eAHT 14S Al und A2 AnaGeo OHNE CAS (Abschnitt 1) Seite 1von5

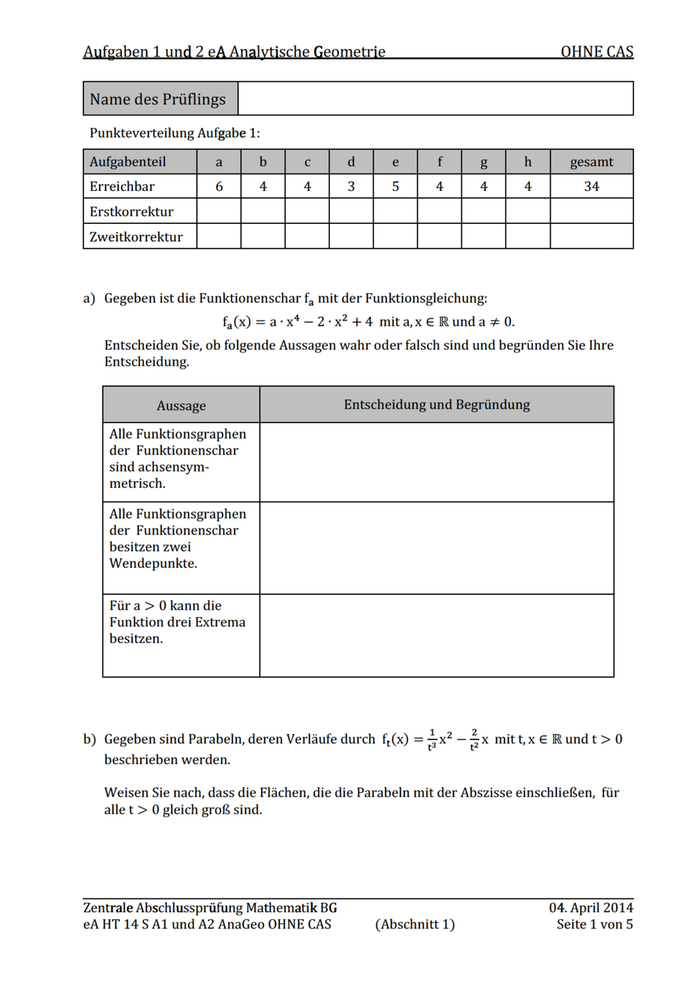
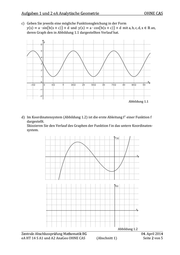
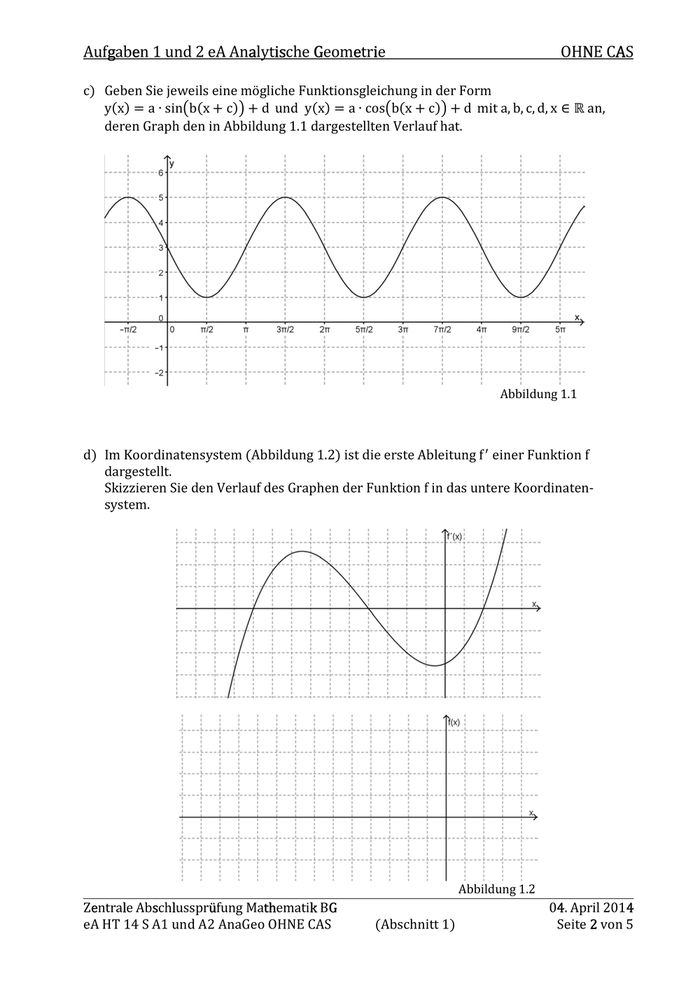
Aufgaben Geometrie g e 1 und 2 eA Analytische a is G e i OHNE N CAS A c) Geben Sie jeweils eine mögliche Funktionsgleichung in der Form y(x) = a ∙ sinLb(x + c)M + d und y(x) = a ∙ cosLb(x + c)M + d mit a, b, c, d, x ∈ ℝ an, deren Graph den in Abbildung 1.1 dargestellten Verlauf hat. Abbildung 1.1 d) Im Koordinatensystem (Abbildung 1.2) ist die erste Ableitung f einer Funktion f dargestellt. Skizzieren Sie den Verlauf des Graphen der Funktion f in das untere Koordinaten- system. O Zentrale Mathematik e l Abschlussprüfung s l ü th k BG G eA HT 14 S A1 und A2 AnaGeo OHNE CAS (Abschnitt 1) Abbildung 1.2 04. 4 April 2014 Seite 2 von 5

Aufsaben 1 und 2 eA Analvtische Geometrie OHNE CAS

e) Ein Quader mit den Eckpunkten E(0|: 2|0) und D(5]2]4) steht auf der x, -x,-Ebene (siehe
Abbildung). Die Länge der Strecke EF beträgt 3 Längeneinheiten.

 

x

e Geben Sie die Koordinaten der Eckpunkte A und Han.

e Ermitteln Sie das Volumen des Quaders.

e Bestimmen Sie eine Gleichung der Ebene durch die Punkte D, Eund Fin
Normalform.

2 k —3k
f) Gegeben sind die Vektoren ä = (>) b= () und€ = ( —2k ) mitkeER.
0 k 3k+2
e Zeigen Sie, dass der Vektor € orthogonal zu den Vektoren ä und bist.
e Untersuchen Sie, ob eseink € R gibt, so dass der Vektor € ein Einheitsvektor ist.

g) Gegeben sind der Punkt A(1|2|1) und eine Menge von Punkten C,(#|k| — 2) mitk ER.

e Beschreiben Sie die Lage der Punkte der Menge C, im Raum und geben Sie hierfür
ein mathematisches Modell an.

e Zeigen Sie, dass kein Punkt der Menge C, von Punkt A einen Abstand vond =4LE
hat.

h) Gegeben sind die Ebene E mit der Ebenengleichung E: x] — 2x2 + 3x3 = 3 sowie die
Geradenschar g, mit der Gleichung

0 a?
8.::X=| a |+tr-| 0 |mitrae Runda #0.

— 1 a
e Erläutern Sie, warum der Parameterwerta = O kein sinnvoller Wert in Hinblick auf
die Geradenschar ist.
e Erläutern Sie, zu welcher Koordinatenebene alle Geraden der Geradenschar g,
parallel verlaufen.
e Geben Sie die Geradengleichung für a= —3 an und untersuchen Sie die
Lagebeziehung der Ebene E und der Geraden g_; .

Zentrale Abschlussprüfung Mathematik BG 04. April 2014
eAHT 14S Al und A2 AnaGeo OHNE CAS (Abschnitt 1) Seite 3 von5

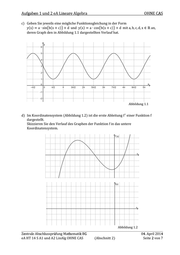
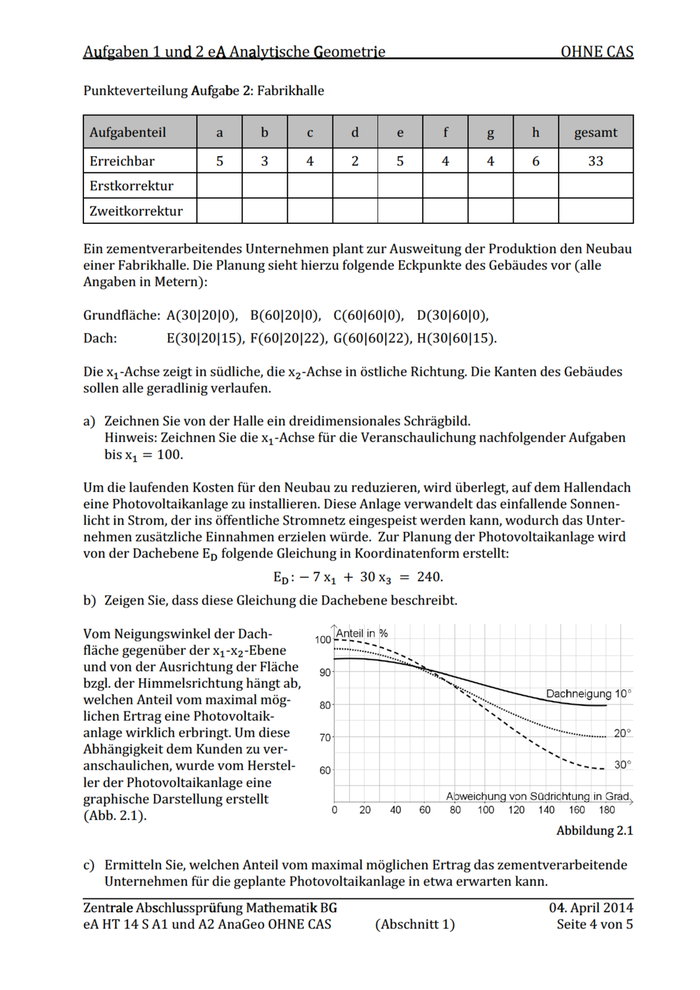
Aufsaben 1 und 2 eA Analvtische Geometrie OHNE CAS

Punkteverteilung Aufgabe 2: Fabrikhalle

EOSBESECSESERESEAFSESE

Erreichbar |

Erstkorrektur Ir rn
Zweitkorrektur | | | [TTS NT

 

Ein zementverarbeitendes Unternehmen plant zur Ausweitung der Produktion den Neubau
einer Fabrikhalle. Die Planung sieht hierzu folgende Eckpunkte des Gebäudes vor (alle
Angaben in Metern):

Grundfläche: A(30|20|0), B(60]20|0), C(60]60]0), D(30]60]0),
Dach: E(30]20]15), F(60]20|22), G(60|60|22), H(30]60|15).

Die x, -Achse zeigt in südliche, die x,-Achse in östliche Richtung. Die Kanten des Gebäudes
sollen alle geradlinig verlaufen.

a) Zeichnen Sie von der Halle ein dreidimensionales Schrägbild.
Hinweis: Zeichnen Sie die x;-Achse für die Veranschaulichung nachfolgender Aufgaben
bisx, = 100.

Um die laufenden Kosten für den Neubau zu reduzieren, wird überlegt, auf dem Hallendach
eine Photovoltaikanlage zu installieren. Diese Anlage verwandelt das einfallende Sonnen-
licht in Strom, der ins öffentliche Stromnetz eingespeist werden kann, wodurch das Unter-
nehmen zusätzliche Einnahmen erzielen würde. Zur Planung der Photovoltaikanlage wird
von der Dachebene Ep folgende Gleichung in Koordinatenform erstellt:

Ep: - 7x1 + 30x3 = 240.
b) Zeigen Sie, dass diese Gleichung die Dachebene beschreibt.

Vom Neigungswinkel der Dach- 100 "Anteil in %
fläche gegenüber der x/-x2-Ebene
und von der Ausrichtung der Fläche
bzgl. der Himmelsrichtung hängt ab,
welchen Anteil vom maximal mög-
lichen Ertrag eine Photovoltaik-
anlage wirklich erbringt. Um diese
Abhängigkeit dem Kunden zu ver-
anschaulichen, wurde vom Herstel-
ler der Photovoltaikanlage eine

 

 

 

graphische Darstellung erstellt Abweichung von Südrichtung in Grad,
(Abb 2 1) 0 20 40 60 80 100 120 140 160 180
Abbildung 2.1

c) Ermitteln Sie, welchen Anteil vom maximal möglichen Ertrag das zementverarbeitende
Unternehmen für die geplante Photovoltaikanlage in etwa erwarten kann.

Zentrale Abschlussprüfung Mathematik BG 04. April 2014
eAHT 14S Al und A2 AnaGeo OHNE CAS (Abschnitt 1) Seite 4 von5

Aufgaben 1 und Geometrie u d 2 eA Analytische a i G i OHNE CAS d) Für die Photovoltaikanlage soll eine elektrische Leitung vom Mittelpunkt M der TTTT verlegt werden, der vom Punkt E einen Dachfläche zu einem Punkt Z der Dachkante EF Abstand von 10 m hat. Berechnen Sie die Koordinaten der Punkte M und Z. Das Grundstück wurde durch das Unternehmen deshalb ausgewählt, da es direkt an das Ufer eines Flusses grenzt. Die transporttechnisch günstige Lage soll dazu genutzt werden, um Rohstoffe per Schiff anzuliefern und mit Hilfe eines geradlinigen Förderbandes zur Hallenwand BCGF zu befördern. Der Anfangspunkt des Förderbandes soll sich am Flussufer im Punkt P(100|70|0) befinden. e) Auf dem Grundstück befindet sich im Punkt S(93|66,5|0) bereits ein 6 m hoher senkrechter Pfeiler, der aufgrund seiner Stabilität sehr gut zum Abstützen des Förderbandes geeignet wäre. Untersuchen Sie, ob es möglich ist, das Förderband vom Punkt P über die Spitze des Pfeilers zur Wand BCGF zu bauen. f) Die Anlage zur Zementverarbeitung im Inneren der Fabrikhalle macht es notwendig, dass das Förderband die Hallenwand im Punkt Q(60|50|20) erreicht. Es muss jedoch sichergestellt werden, dass der Punkt Q zur Dachfläche einen Abstand von mindestens 1,5 m hat. Entscheiden Sie, ob diese Bedingung erfüllt ist. g) Die Planung des Förderbandes vom Punkt P(100|70|0) zum Punkt Q(60|50|20) sieht vor, dass im Punkt T(68|54|0) das Fundament für einen senkrechten Stützpfeiler gegossen wird. Zeigen Sie, dass die Lage vom Punkt T hierfür geeignet ist. Die Leistung des geplanten Förderbandes (gemessen in Tonnen (t) pro Stunde (h)) vom Punkt P(100|70|0) zum Punkt Q(60|50|20) beträgt laut Herstellerangaben bei waage- rechtem Verlauf 800 t/h. Bei schrägem Verlauf ist die Leistung jedoch geringer. Zur Berechnung der Förderbandleistung ist der maximale Leistungswert von 800 t/h mit einem Faktor c zu multiplizieren, der vom Neigungswinkel α des Förderbandes gegenüber der Horizontalen abhängt. Laut Herstellerangaben kann der Faktor c für Winkel bis maximal 44° mithilfe folgender ganzrationaler Funktion berechnet werden: c(α) = −0,0005 α + 1 mit α ∈ ℝ und 0 ≤ α ≤ 44 8 h) Zeigen Sie, dass es länger als 10 Stunden dauern würde, einen Zementfrachter mit einer Ladung von 6000 t zu entladen. Bestimmen Sie, welchen Neigungswinkel das Förderband maximal haben darf, um eine Entladezeit von höchstens 10 Stunden zu erreichen. Zentrale ra e Abschlussprüfung s u ü u Mathematik t a k BG G eA HT 14 S A1 und A2 AnaGeo OHNE CAS (Abschnitt 1) 04. 4 April 2014 Seite 5 von 5

Aufsaben 1 und 2 eA Lineare Alsebra OHNE CAS

m

Punkteverteilung Aufgabe 1:

Sana PERF LBeRTee
EFF
ziwonen | III FPTRRT

a) Gegeben ist die Funktionenschar f, mit der Funktionsgleichung:

emeican [slalela

 

f,.&)=a'x*-2:x?+4 mitaxeRunda +0.

Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind und begründen Sie Ihre
Entscheidung.

Entscheidung und Begründung

Alle Funktionsgraphen
der Funktionenschar
sind achsensym-
metrisch.

Für a > 0 kann die
Funktion drei Extrema
besitzen.

Alle Funktionsgraphen
der Funktionenschar
besitzen zwei
Wendepunkte.

 

b) Gegeben sind Parabeln, deren Verläufe durch f;(x) = —x2 _ 5x mit,xe Rundt>0
beschrieben werden.

Weisen Sie nach, dass die Flächen, die die Parabeln mit der Abszisse einschließen, für
allet > 0 gleich groß sind.

Zentrale Abschlussprüfung Mathematik BG 04. April 2014
eAHT 14S Al und A2 LinAlg OHNE CAS (Abschnitt 2) Seite 1von 7

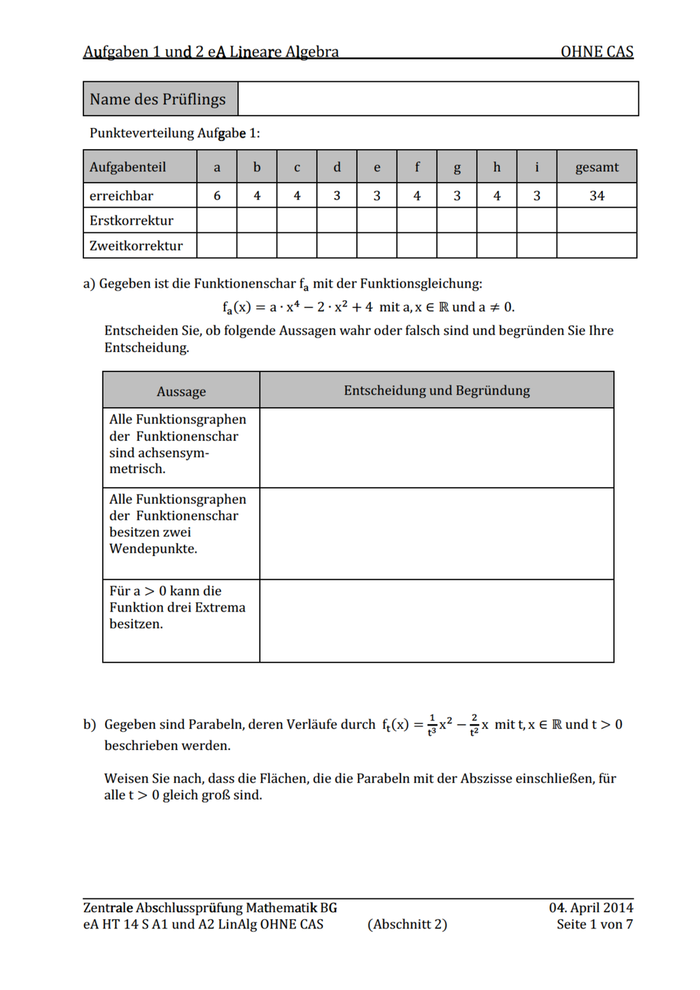
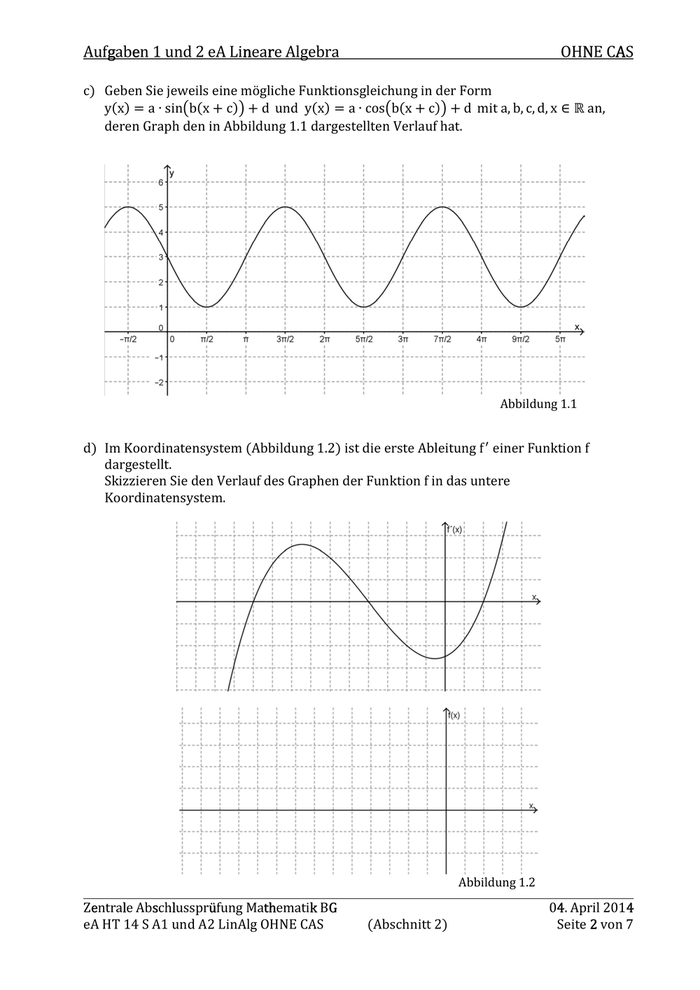
Aufgaben g e 1 und 2 eA Lineare n r Algebra OHNE N CAS A c) Geben Sie jeweils eine mögliche Funktionsgleichung in der Form y(x) = a ∙ sinLb(x + c)M + d und y(x) = a ∙ cosLb(x + c)M + d mit a, b, c, d, x ∈ ℝ an, deren Graph den in Abbildung 1.1 dargestellten Verlauf hat. Abbildung 1.1 d) Im Koordinatensystem (Abbildung 1.2) ist die erste Ableitung f einer Funktion f dargestellt. Skizzieren Sie den Verlauf des Graphen der Funktion f in das untere Koordinatensystem. O Zentrale Mathematik e l Abschlussprüfung s l ü th k BG G eA HT 14 S A1 und A2 LinAlg OHNE CAS (Abschnitt 2) Abbildung 1.2 04. 4 April 2014 Seite 2 von 7

Aufsaben 1 und 2 eA Lineare Alsebra OHNE CAS

e) Berechnen Sie die fehlenden Matrixelemente a,b, c € R zur folgenden Matrizen-

multiplikation:
1 4 2 1 -N_ 6 1-9
2 2) '\, p J=l-e - -e}
> 15
00x
f) Gegeben ist die Mara = (y 0 ) mitx,y‚zeR.
002

001
Ermitteln Sie, welche Werte x, y und zannehmen müssen, damit Q? = ( 0 ı) gilt.

g) Bestimmen Sie die Koeffizienten a,bundcmita,b,ce Rso, dass das folgende lineare
Gleichungssystem die Lösung L = {(3] —4 | 2 )} hat.

ax—- y-%z = 1
tb y4H7 2 =D
3-x+tb’y+tb-z 5

h) Bestimmen Sie aus den folgenden Matrizengleichungen jeweils die Matrix X.
(Für alle Matrizen existieren die zugehörigen inversen Matrizen, se R.)

E=X-AT-B-4.X-C

 

Zentrale Abschlussprüfung Mathematik BG 04. April 2014
eAHT 14S Al und A2 LinAlg OHNE CAS (Abschnitt 2) Seite 3 von 7

Aufsaben 1 und 2 eA Lineare Alsebra OHNE CAS

i) Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind.

Hinweis: Für jedes richtige Kreuz gibt es einen Punkt, für jedes falsche Kreuz gibt es
null Punkte, nicht angekreuzte Zeilen bleiben neutral (null Punkte).

Die Multiplikation der Matrizen A und B ergibt die Einheitsmatrix.

-5
A=(\ % \,) und »- (5 -)

2 -3
4 -5
Die Matrix B= ( ) ist die Inverse der Matrix A = (
2 -3
Unter der Voraussetzung, dass die Matrizen C und D invertierbar sind,
soll folgende Aussage gelten:
Wenn X = C’!- Dt gilt, dann gilt: x"!=C-D.

7 1
10 -2

 

Zentrale Abschlussprüfung Mathematik BG 04. April 2014
eAHT 14S Al und A2 LinAlg OHNE CAS (Abschnitt 2) Seite 4 von 7

Aufgaben 1 und 2 eA Lineare Algebra OHNE CAS

Punkteverteilung Aufgabe 2: Kundenzufriedenheit

Augbensn [a [5 Te fa fe ee Te Tg
ETTSEFENSENENENERESNENBENE

ontomaaı | | I I I FT
zweikomekon | | | | | | I I

Das Möbelhaus „Schanz“ beauftragt ein Marktforschungsunternehmen die Kundenzufrie-
denheit mit den monatlich wechselnden Sonderangeboten zu untersuchen. Anhand von Er-
fahrungen bereits erfolgter Untersuchungen von 2000 Kunden kann das Marktforschungs-
unternehmen die monatliche Änderung der Kundenzufriedenheit wie folgt darstellen:

 

S & sehr zufrieden

U £ unzufrieden

Z. & zufrieden

 

Abbildung 2.1

a) Erläutern Sie anhand eines ausgewählten Elementes der Matrix A, warum diese Matrix
das Änderungsverhalten der Kundenzufriedenheit wiedergibt.

S U Z

S /0,60 0,45 0,30
A=U BE 0,55 020)
z\025 0 0,0

Zu Beginn der Untersuchung wurden insgesamt 2000 Kunden befragt. Das Änderungsver-

halten bezüglich der Kundenzufriedenheit wird durch die Matrix A und die Verteilung der
S

Kunden wird durch den Vektor v = B beschrieben. Von diesen befragten Kunden waren

z
ein Fünftel aller Kunden sehr zufrieden mit den monatlich wechselnden Sonderangeboten

und die Hälfte aller Kunden war mit diesen Angeboten unzufrieden.

b) Berechnen Sie, wie viele Kunden nach dem ersten Monat sehr zufrieden und wie viele
Kunden unzufrieden mit den wechselnden Sonderangeboten waren.

Bestimmen Sie auch die fehlenden Daten in der Tabelle 2.1 (Seite 6).

Zentrale Abschlussprüfung Mathematik BG 04. April 2014
eAHT 14S Al und A2 LinAlg OHNE CAS (Abschnitt 2) Seite 5 von 7