Mathematik_BG_eA_HT_2016_geschwrzt.pdf
Dieses Dokument ist Teil der Anfrage „BG Abiturklausuren 2013-2019 SH“
Aufgaben 1 und 2 Analytische Geometrie eA Punkteverteilung Aufgabe 1: [Aufgabenteit | a | 5 | ce | a | e | 5 | 8 | m | gesam [Erstkorrektur | | | | (Zweitkorrektur | | | Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter: a,b,c,... € Runddie Variablen: x,t,... ER. a) Gegeben ist die Gleichung der abschnittsweise definierten Funktion f,, mit: 1,5x?-5x+3 fürx<s3 = <3, 2%) a'x+b fürx>3 al) Bestimmen Sie die Gleichung der 1. Ableitung der Funktion f,p- a2) Bestimmen Sie die Koeffizienten a und b so, dass der Graph von f,, sprung- und knickfrei verläuft. a3) Zeigen Sie, dass die Gleichung: S f„, (x) dx = —1 für den Parameter k = 1 erfüllt ist. b) Entscheiden Sie ausgehend von der Funktion f mit der Gleichung: = a: sin(b (x - c)) +dmit ,b#0, ob die folgenden Aussagen wahr oder falsch sind. Hinweis: Für jedes richtige Kreuz gibt es einen Punkt, für jedes falsche Kreuz gibt es null Punkte, nicht angekreuzte Zeilen bleiben neutral (null Punkte). Die Funktion F mit der Gleichung: F(x) = — = . cos(b :.(x— c)) +d'x+te ist eine Stammfunktion der Funktion f. Wenna=b=1undc=d = Ogilt, so befindet sich eine maximale, positive Änderungsrate beix = n. Wenna=b=1,c=0undd > 0 gilt, beträgt der Integralwert über eine Periodenlänge von der Funktion f immer null. Füra=3,b=2undc=d = Ogilt: Die Periodenlänge beträgt p = 2n. Fürb = 1 und c = O beschreiben die Gleichungen der Funktionen fund g mit: g(x) =a:cos|b- (x _ =) + .d den gleichen Funktionsgraphen. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 eAHT 16 S Al und A2 AnaGeo (Abschnitt 1) Seite 1 von 6
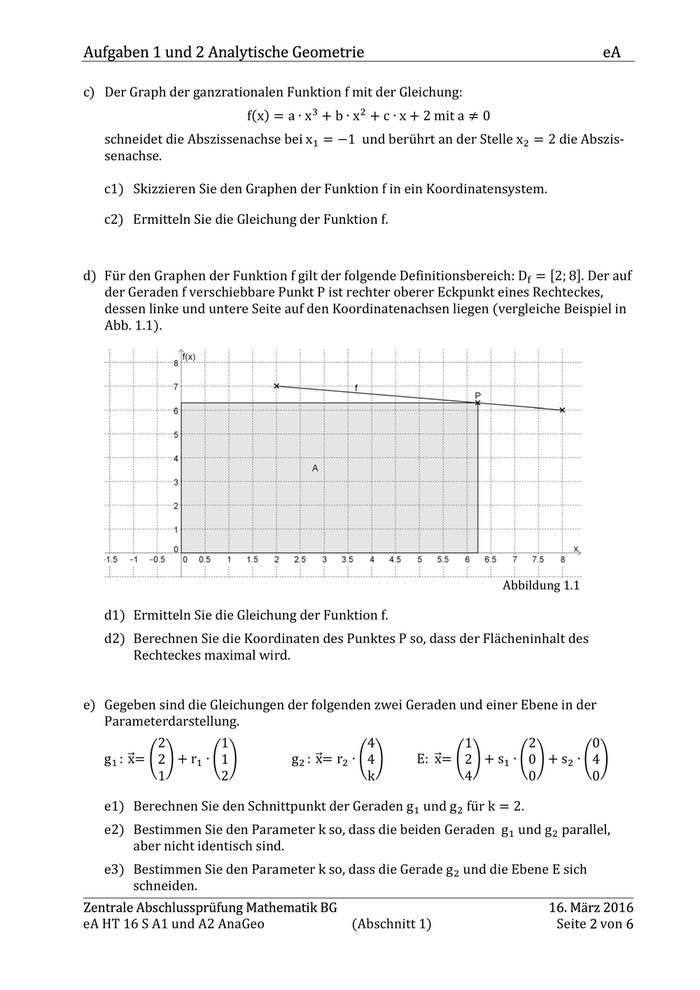
Aufgaben 1 und 2 Analytische Geometrie eA c) Der Graph der ganzrationalen Funktion f mit der Gleichung: f(x) = a ∙ x + b ∙ x + c ∙ x + 2 mit a ≠ 0 S < schneidet die Abszissenachse bei xT = −1 und berührt an der Stelle x< = 2 die Abszis- senachse. c1) Skizzieren Sie den Graphen der Funktion f in ein Koordinatensystem. c2) Ermitteln Sie die Gleichung der Funktion f. d) Für den Graphen der Funktion f gilt der folgende Definitionsbereich: DU = V2; 8Y. Der auf der Geraden f verschiebbare Punkt P ist rechter oberer Eckpunkt eines Rechteckes, dessen linke und untere Seite auf den Koordinatenachsen liegen (vergleiche Beispiel in Abb. 1.1). Abbildung 1.1 d1) Ermitteln Sie die Gleichung der Funktion f. d2) Berechnen Sie die Koordinaten des Punktes P so, dass der Flächeninhalt des Rechteckes maximal wird. e) Gegeben sind die Gleichungen der folgenden zwei Geraden und einer Ebene in der Parameterdarstellung. 2 1 gT : [x\= ]2^ + rT ∙ ]1^ 1 2 4 g < : [x\= r< ∙ ]4^ k 1 2 0 E: x[\= ]2^ + sT ∙ ]0^ + s< ∙ ]4^ 4 0 0 e1) Berechnen Sie den Schnittpunkt der Geraden gT und g < für k = 2. e2) Bestimmen Sie den Parameter k so, dass die beiden Geraden gT und g < parallel, aber nicht identisch sind. e3) Bestimmen Sie den Parameter k so, dass die Gerade g < und die Ebene E sich schneiden. Zentrale Abschlussprüfung Mathematik BG eA HT 16 S A1 und A2 AnaGeo (Abschnitt 1) 16. März 2016 Seite 2 von 6
Aufgaben 1 und 2 Analytische Geometrie eA f) Gegeben sind die Ebenen E, und E, mit den folgenden Gleichungen: E1:3x- 4y + 62 =-2 und Ez:2x- 2y + 32 = 2. Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind. Hinweis: Für jedes richtige Kreuz gibt es einen Punkt, für jedes falsche Kreuz gibt es null Punkte, nicht angekreuzte Zeilen bleiben neutral (null Punkte). Die Ebene Ez mit der Gleichung: 2x - 2y + 3z = —2 und die Ebene E, sind identisch. Der Punkt B(4|0| — 2) liegt in der Ebene E,, aber nicht in der Ebene E.. Die Ebene E, schneidet die y-Achse in dem Punkt S,(0|1,5]0). 1 Die Gleichung —1,5x - 2y + 3z =-2 beschreibt auch die Ebene E,. Ein Normalenvektor der Ebene E, ist der Vektor n i-( 7 ) g) Die Punkte D(2|-4]| — 3), E(4|-1|3) und F(5]|2] — 1) bilden die Eckpunkte eines Dreiecks. Prüfen Sie rechnerisch, ob es sich dabei um ein gleichschenkliges oder gleichseitiges Dreieck handelt. h) Gegeben sind die Ebenen E, und Ezmit den Gleichungen: Fr —2 Der Vektor NE, = ( 2) ist ein Normalenvektor der Ebene E,. —2 h1) Geben Sie jeweils eine Gleichung der Ebene E, in Koordinaten- und Parameterform an. h2) Ermitteln Sie den Wert des Parameters a, so dass die Normalenvektoren der Ebenen E, und E;, linear abhängig sind. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 eAHT 16 S Al und A2 AnaGeo (Abschnitt 1) Seite 3 von 6

Aufgaben 1 und 2 Analytische Geometrie eA Punkteverteilung Aufgabe 2: AirRace Autabenen Ta Ts TefafelrTefnfı Tom (ereictar al alolslals|sleale| o ertomeger | | I I | I I Zwekomesur | | | | | | | [| | I Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter: a,b,c,... € Runddie Variablen: x,t,... ER. Beim AirRace geht es darum, möglichst schnell mit einem Flugzeug einen Parcours abzu- fliegen. Dieser wird durch sogenannte „Air Gates“, mindestens 15 m breite Tore, markiert. Die „Air Gates“ bestehen aus 20 m hohen Pylonen (aus Stoff gefertigte und mit Luft gefüllte seitliche Begrenzungen der Flugstrecke). Zusätzlich müssen die Piloten bestimmte, vorge- gebene Manöver fliegen, für die anschließend von Schiedsrichtern Punkte vergeben werden. Im gesamten Rennen darf eine Flughöhe von 10 m nicht unterschritten werden, im Allgemeinen wird auf einer Höhe von 15 m geflogen. Es wird im Wettkampf nur über Was- serflächen geflogen (alle Angaben sind in Metern). Die anschließende Graphik (Abb. 2.1) zeigt den Parcours und eine Flugroute. o Werbeballon z Tr EEE Rense] = Zuschauer BA a \ er B -tribüne _- 2 Airgate I Airgate A H DD. u. ; . Abbildung 2.1 Ansicht des Parcours Jedes Airgate wird durch zwei Pylonen begrenzt. Die Fußpunkte der Pylonen der Airgates A, B und € können Sie der Tabelle 2.1 entnehmen: A, (600110010 A, (615|105|0 B}(450|550]0 B,(465|555]0 C,(395]305]0 C,(405|295]0 Tabelle 2.1 Die Angaben der Punkte in Tabelle 2.1 beziehen sich auf die Mitte der Fußpunkte der Pylonen. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 eAHT 16 S Al und A2 AnaGeo (Abschnitt 1) Seite 4 von 6
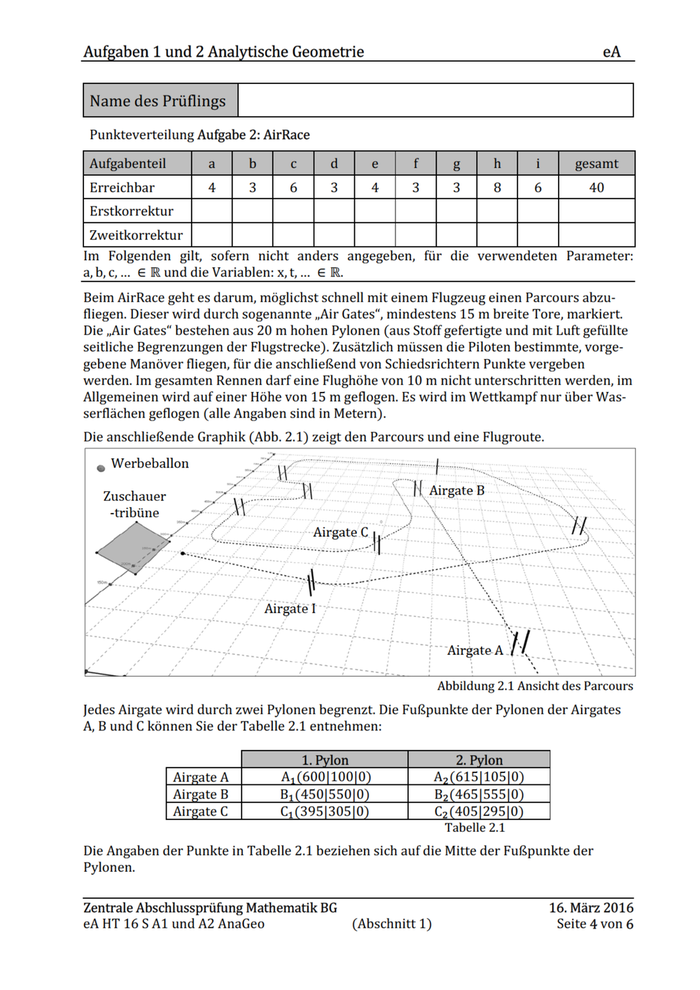
Aufgaben 1 und 2 Analytische Geometrie Als erste Aufgabe sind vom Piloten nacheinander die Airgates A und B (Abb. 2.1) zu durchfliegen. Dafür darf er nicht länger als 5 Sekunden benötigen. eA a) Begründen Sie, dass sich die entsprechende Flugroute mit der folgenden Gleichung 607,5 −150 h: [x\ = ] 102,5^ + r ∙ ] 450 ^ 15 0 beschreiben lässt, wenn davon ausgegangen wird, dass die Airgates mittig zwischen den Pylonen durchflogen werden. b) Ermitteln Sie die Geschwindigkeit in Kilometer pro Stunde, mit der der Pilot mindes- tens fliegen muss, um diese erste Aufgabe zu erfüllen. Im Anschluss daran absolviert der Pilot einen Steigflug mit mehreren Pirouetten (nicht in Abb. 2.1 dargestellt). Nach Abschluss dieser Manöver befindet er sich im Punkt P(800|700|300). Von hier aus muss er das Airgate C auf einer Höhe von höchstens 20 m und mindestens 10 m passieren. Dazu fliegt er in Richtung des Vektors: −80 v [\ = ]−80^. −57 c) Weisen Sie rechnerisch nach, dass der Pilot das Airgate C in einer Höhe von höchstens 20 m und mindestens 10 m passiert. Der Pilot kann den Sinkflug bei einer solchen Höhe nur dann abfangen, wenn der Schnitt- winkel in dieser Situation gegenüber der Wasseroberfläche beim Passieren des Airgates nicht größer als 30° ist. (Die Wasseroberfläche wird in diesem Fall als plane Fläche mit der Höhe z = 0 betrachtet.) d) Prüfen Sie, ob der Pilot die Maschine noch rechtzeitig abfangen kann. Die Zuschauertribüne lässt sich durch die Koordinaten der Eckpunkte TT (20|180|0), T< (10|280|0), T3(−40|275|40) und Ts (−30|175|40) beschreiben (siehe Abb. 2.1). e) Begründen Sie, dass die Ebene E mit der Ebenengleichung: −50 10 10 E: [x\ = d280e + s ∙ d−100e + t ∙ ] −5 ^ mit 0 ≤ s ≤ 1 und 0 ≤ t ≤ 1 0 0 40 die Zuschauertribüne beschreibt. f) Ermitteln Sie die Zuschauerkapazität der Tribüne unter der Maßgabe, dass pro Sitz- platz 0,75 m² berücksichtigt und 20 % der Gesamtfläche für Aufgänge benötigt werden. Zentrale Abschlussprüfung Mathematik BG eA HT 16 S A1 und A2 AnaGeo (Abschnitt 1) 16. März 2016 Seite 5 von 6

Aufgaben 1 und 2 Analytische Geometrie eA Als Werbeträger hat der Hauptsponsor einen großen, kugelförmigen Ballon ausgebracht. Dieser mit Helium befüllte Ballon wird mit Hilfe einer Gasflasche befüllt und soll mittig über den Sitzflächen der Zuschauertribüne mithilfe eines Seils befestigt werden. Die Höhe des Zentrums des Ballons senkrecht (lotrecht) über der Wasseroberfläche (z = 0) soll 270 m betragen. Der Ballon hat einen Durchmesser von 10 m und das Seil ist an seiner Unterseite befestigt. g) Berechnen Sie die Koordinaten des Zentrums des kugelförmigen Ballons und die Länge des Seils, das für die Befestigung des Ballons an der Zuschauertribüne benötigt wird. Zum Abschluss durchfliegt der Pilot mittig das Airgate I im Punkt I, (320]177,5]15) und hält dann zum Abschied in Richtung des Punktes Q (100]200]15) direkt auf die Zuschauertribüne zu. Die Regularien besagen, dass ein quaderförmiger Sicher- heitsbereich um die Tribüne nicht durch- flogen werden darf (siehe Abb. 2.2). Der gekennzeichnete Sicherheitsabstand s von der oberen und seitlichen Begrenzung der Tribüne beträgt dabei 150 m. Abbildung. 2.2: quaderförmiger Sicherheitsbereich h) Berechnen Sie den Punkt, in dem der Pilot bei gleichbleibender Flugroute in diesen Sicherheitsbereich (in diesem Fall die direkt 150 Meter in Sichtrichtung der Zuschauer vor der Tribüne liegende Begrenzungsebene) einfliegen und damit nachträglich disqualifiziert werden würde. Um nicht disqualifiziert zu werden, behält der Werbeballon Pilot zwar den Kurs grundsätzlich bei, aber befindet sich genau ab Durchflug des Airgates I in einem Steigflug mit einer Steigung von 120 %. i) Zeigen Sie, dass der minimale Abstand, mit dem der Pilot bei unverändertem Steigflug den kugelförmigen Werbeballon mit einem Durchmesser von 10 m passieren wird, ca. 142,87 m beträgt. Es wird davon ausge- Zuschauer- gangen, dass das Zentrum (der Mittelpunkt) tribüne des Ballons sich nun im Punkt Z(0[210|170) befindet. Abbildung 2.3: Ansicht der Zuschauertribüne Zentrale Abschlussprüfung Mathematik BG 16. März 2016 eAHT 16 S Al und A2 AnaGeo (Abschnitt 1) Seite 6 von 6

Aufgaben 1 und 2 Lineare Algebra eA Punkteverteilung Aufgabe 1: unanenen Ta ]»Tefafelefs]n Sem reiner | ss |s[s|[s|s|s|s. ensonsar I I I III rer zwwonan | I I LI TPPI Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter: a,b,c,... € Runddie Variablen: x,t,... ER. a) Gegeben ist die Gleichung der abschnittsweise definierten Funktion fz», mit: 1,5x?-5x+3 fürx<s3 = ft <3, 2%) a'x+b fürx>3 al) Bestimmen Sie die Gleichung der 1. Ableitung der Funktion fzp- a2) Bestimmen Sie die Koeffizienten a und b so, dass der Graph von f,, sprung- und knickfrei verläuft. a3) Zeigen Sie, dass die Gleichung: E f,», (x) dx = —1 für den Parameter k = 1 erfüllt ist. b) Entscheiden Sie ausgehend von der Funktion f mit der Gleichung: f(x) = a: sin(b . (x -c)) +dmit ,b#0, ob die folgenden Aussagen wahr oder falsch sind. Hinweis: Für jedes richtige Kreuz gibt es einen Punkt, für jedes falsche Kreuz gibt es null Punkte, nicht angekreuzte Zeilen bleiben neutral (null Punkte). Die Funktion F mit der Gleichung: F(x) = — z . cos(b (x - c)) +d’x+e ist eine Stammfunktion der Funktion f. Wenna=b=1undc=d = Ogilt, so befindet sich eine maximale, positive Änderungsrate beix = n. Wenna=b=1,c=0undd > 0 gilt, beträgt der Integralwert über eine Periodenlänge von der Funktion f immer null. Füra=3,b=2undc=d = Ogilt: Die Periodenlänge beträgt p = 2n. Fürb = 1undc = O beschreiben die Gleichungen der Funktionen fund g T mit: g(x) =a:cos|b- (x _ =) + d den gleichen Funktionsgraphen. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 eAHT 16S Al und A2 LinAlg (Abschnitt 2) Seite 1 von 6
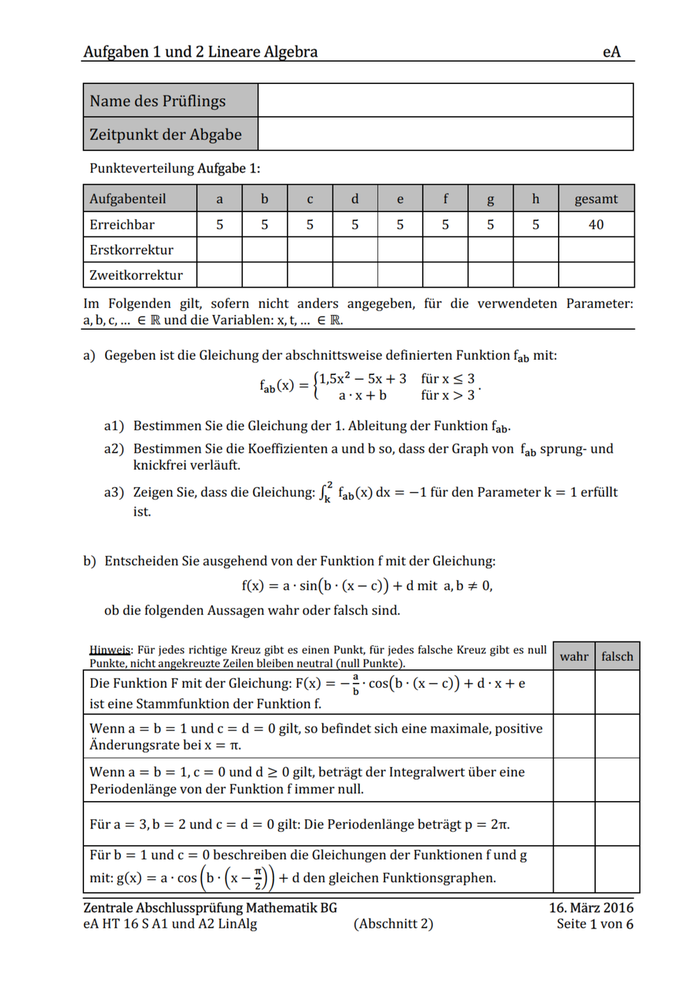
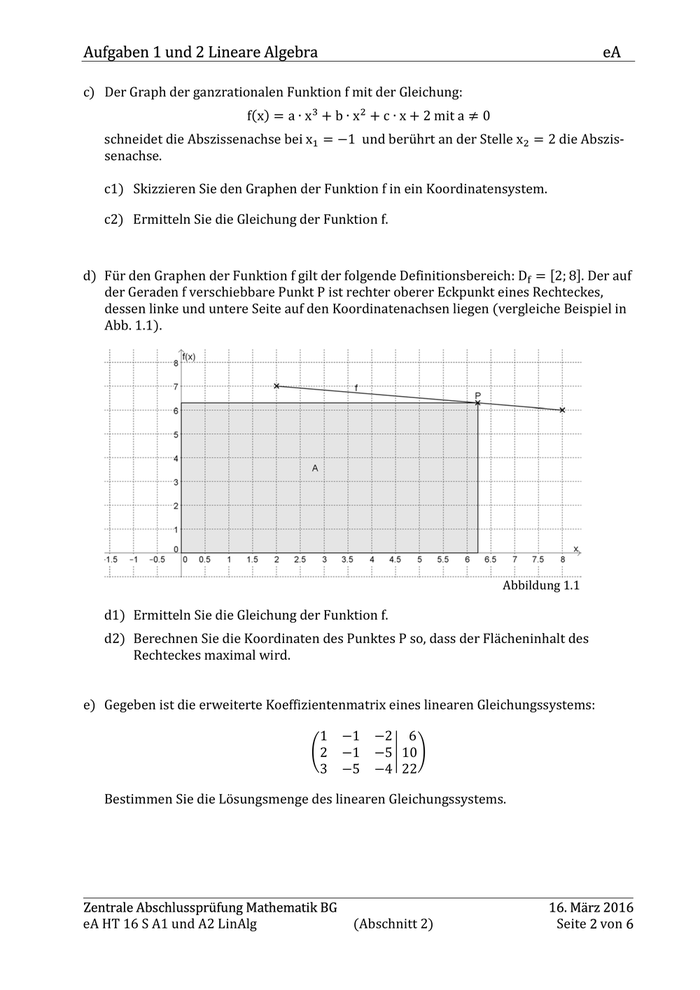
Aufgaben 1 und 2 Lineare Algebra eA c) Der Graph der ganzrationalen Funktion f mit der Gleichung: f(x) = a ∙ x + b ∙ x + c ∙ x + 2 mit a ≠ 0 S < schneidet die Abszissenachse bei xT = −1 und berührt an der Stelle x< = 2 die Abszis- senachse. c1) Skizzieren Sie den Graphen der Funktion f in ein Koordinatensystem. c2) Ermitteln Sie die Gleichung der Funktion f. d) Für den Graphen der Funktion f gilt der folgende Definitionsbereich: DU = V2; 8Y. Der auf der Geraden f verschiebbare Punkt P ist rechter oberer Eckpunkt eines Rechteckes, dessen linke und untere Seite auf den Koordinatenachsen liegen (vergleiche Beispiel in Abb. 1.1). d1) Ermitteln Sie die Gleichung der Funktion f. Abbildung 1.1 d2) Berechnen Sie die Koordinaten des Punktes P so, dass der Flächeninhalt des Rechteckes maximal wird. e) Gegeben ist die erweiterte Koeffizientenmatrix eines linearen Gleichungssystems: 1 −1 −2 6 ]2 −1 −5 10^ 3 −5 −4 22 Bestimmen Sie die Lösungsmenge des linearen Gleichungssystems. Zentrale Abschlussprüfung Mathematik BG eA HT 16 S A1 und A2 LinAlg (Abschnitt 2) 16. März 2016 Seite 2 von 6
Aufgaben 1 und 2 Lineare Algebra eA f) Gegeben sind die folgenden Matrizen: 1-10 -1 0 4 10-1 1-(0 0 2), 8-( 1 0). c=( n und o=(-ı 0 0) 100 00 02 0 Entscheiden Sie, welche der folgenden Aussagen wahr bzw. falsch sind. Hinweis: Für jedes richtige Kreuz gibt es einen Punkt, für jedes falsche Kreuz gibt es null Punkte, nicht angekreuzte Zeilen bleiben neutral (null Punkte). Für die Matrix D gilt: D = AT. — Die Rechenoperation A - B — B ist definiert. — Zur Matrix C existiert die inverse Matrix C=! und esgilt: ı_f7il = Es gilt: C" = E mitn € Nundn > 2, wobei die Matrix E die Einheits- matrix ist. g) Gegeben sind die Matrizen: 0s 0 64 u=() 2 B.-(-2 1 =) war (-2 5) 013 1 3 g1) Berechnen Sie Q, 'Ps=M.. g2) Bestimmen Sie den Wert für s derart, dass für die Matrix Ms = (7; > 15) gilt. g3) Entscheiden und begründen Sie, ob die Matrizen Q,-Rund QT - RT vom gleichen Typ sein können. h) Gegeben ist die Matrizengleichung A-X + B = AT sowie die Matrix A = (0 u (Alle gegebenen Matrizen sind invertierbar und vom gleichen Typ.) h1) Stellen Sie die gegebene Matrizengleichung nach der Matrix X um. h2) Berechnen Sie die Matrix A”! in Abhängigkeit vom Parameter k. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 eAHT 16S Al und A2 LinAlg (Abschnitt 2) Seite 3 von 6

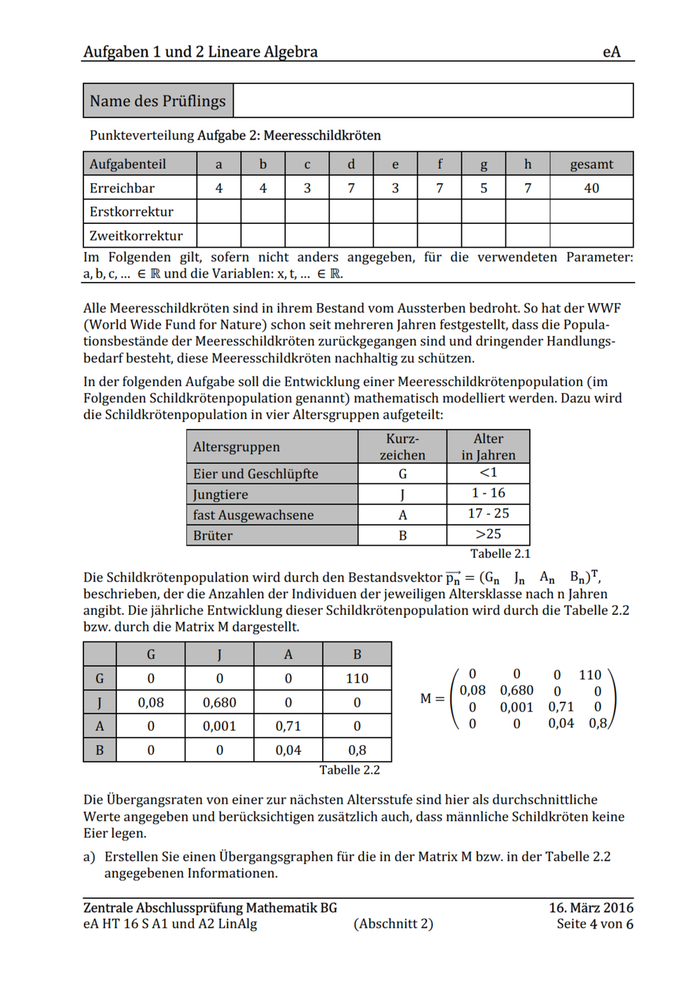
Aufgaben 1 und 2 Lineare Algebra eA Punkteverteilung Aufgabe 2: Meeresschildkröten Aufgabenteil | a | bc Erreichbar | 4 | a a | 7 [3 | 7 | 5 | 7 | 0 4 3 3 7 5 7 40 store | | I I PR Zweier | | I IL III Im Folgenden gilt, sofern nicht anders angegeben, für die verwendeten Parameter: a,b,c,... € Rund die Variablen: x,t,.... ER. Alle Meeresschildkröten sind in ihrem Bestand vom Aussterben bedroht. So hat der WWF (World Wide Fund for Nature) schon seit mehreren Jahren festgestellt, dass die Popula- tionsbestände der Meeresschildkröten zurückgegangen sind und dringender Handlungs- bedarf besteht, diese Meeresschildkröten nachhaltig zu schützen. In der folgenden Aufgabe soll die Entwicklung einer Meeresschildkrötenpopulation (im Folgenden Schildkrötenpopulation genannt) mathematisch modelliert werden. Dazu wird die Schildkrötenpopulation in vier Altersgruppen aufgeteilt: Tabelle 2.1 Die Schildkrötenpopulation wird durch den Bestandsvektor 5 = (Gn Jn An Bun)", beschrieben, der die Anzahlen der Individuen der jeweiligen Altersklasse nach n Jahren angibt. Die jährliche Entwicklung dieser Schildkrötenpopulation wird durch die Tabelle 2.2 bzw. durch die Matrix M dargestellt. 0 0 0 110 0,08 0,680 O0 0 0 0,001 0,771 0 A| 0 | om | om | 0 00 004 08 Bl 0 | 0 Jon | 08 | Tabelle 2.2 Die Übergangsraten von einer zur nächsten Altersstufe sind hier als durchschnittliche Werte angegeben und berücksichtigen zusätzlich auch, dass männliche Schildkröten keine Eier legen. a) Erstellen Sie einen Übergangsgraphen für die in der Matrix M bzw. in der Tabelle 2.2 angegebenen Informationen. Zentrale Abschlussprüfung Mathematik BG 16. März 2016 eAHT 16S Al und A2 LinAlg (Abschnitt 2) Seite 4 von 6